摘要:列生成是用于求解大規模線性優化問題的一種算法,其實就是單純形法的一種形式。如果需要求得整數最優解需要結合分支定界算法。子問題用于生成新的切割方案列,子問題的約束對應切割約束。
列生成是用于求解大規模線性優化問題的一種算法,其實就是單純形法的一種形式。單純性可以通過不斷迭代,通過換基變量的操作,最終找到問題的最優解。但是當問題的規模很大之后,變量的個數就會增大到在有限時間內無法有效迭代求解。所以可以用列生成方法求解,列生成方法可以一開始不列舉所有的列,通過不斷給模型中加入列的方式,最終找到全部解,其關鍵點就是加新列的過程,可以只加入能讓目標值更優的列,從而減少變量的使用個數。
列生成算法流程
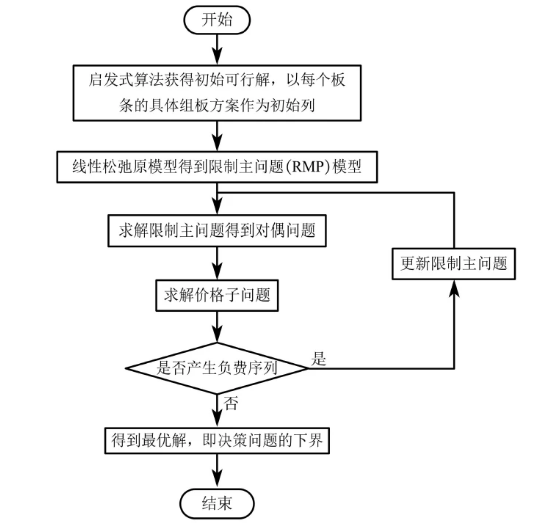
列生成過程中,需要將問題建模為主問題+子問題的形式。
主問題:就是原問題,主要用于決策是否選用某些方案(列)
主問題松弛問題:將主問題變量范圍正整數松弛到正數
限制主問題:主問題去掉一部分列
限制主問題對偶問題:對限制主問題求對偶
價格子問題:原問題的局部問題,用于生成新的方案(列)
求解Cutting Stock問題
問題描述:
將一些鋼管切割成為需要的長度以滿足客戶需求,要求使用的鋼管最少。
每根鋼管長度L=16m
需求:3m鋼管25根;6m鋼管20根,7米鋼管18根
模型建立
主問題
/[min/sum_{j /in J} x_{j}//s.t./qquad/qquad/qquad/qquad/qquad///sum_{j /in J} x_j a_{ij} /ge d_i /qquad /forall i /in I//x_j /in Z /qquad /qquad /quad /forall j /in J /]
/(x_j/): 方案選用的個數
/(a_{ij}/): 方案/(j/)中鋼管/(i/)的個數
/(d_i/): 鋼管/(i/)的需求量
主問題松弛問題
/[min/sum_{j /in J} x_{j}//s.t./qquad/qquad/qquad/qquad/qquad///sum_{j /in J} x_j a_{ij} /ge d_i /qquad /forall i /in I//x_j /ge 0 /qquad /qquad /quad /forall j /in J /]
變量是整數的情況下無法用列生成法求得最優解,需要將問題松弛。如果需要求得整數最優解需要結合分支定界算法。
限制主問題
/[min/sum_{j /in J} x_{j}//s.t./qquad/qquad/qquad/qquad/qquad///sum_{j /in J} x_j a_{ij} /ge d_i /qquad /forall i /in I//x_j /ge 0 /qquad /qquad /quad /forall j /in /Omega_j /]
將主問題中的變量規模減小,一開始只加入一部分可行的切割方案(/(a_j/),列),列生成就是不斷生成新的/(a_j/) 加入到問題中。判斷一個列是否可以加入到問題,需要判斷檢驗數/(/sigma_j = c_j - c_B B^{-1}a_j/),如果檢驗數為負,就可以將新的列加入。其中/(c_BB^{-1}/)有兩重含義:
- 通過限制主問題求得的影子價格
- 通過限制主問題求得的對偶變量
對偶問題和原問題有同樣的最優解,將原問題進行對偶,可以把原問題的變量轉化為約束、約束轉化為變量,因此,對于變量很多的問題將其轉化為對偶問題可以很容易得到其子問題。
對偶問題
/[max /sum_{i /in I} d_i v_i //s.t./qquad/qquad/qquad/qquad/qquad///sum_{i in / I} a_{ij} v_i /le 1 /qquad /qquad /forall j /in /Omega_j //v_j /ge 0 /qquad /qquad /qquad /quad/forall i /in I /]
對偶問題用于推導子問題。可以進入主問題的列,就是檢驗數為負數的列,對于對偶問題,就是違反了約束的列。對偶問題中只有一個約束,/(/sum_{i in / I} a_{ij} /lambda_i /le 1/)可以寫成/(1-/sum_{i /in I} a_i /lambda_i /ge 0/),求其最小值,如果最小值小于0,則說明其違反了約束。子問題用于生成新的切割方案(列),子問題的約束對應切割約束。
子問題
/[min /quad 1-/sum_{i /in I} a_i v_i //s.t./qquad/qquad/qquad/qquad/qquad///sum_{i /in I} a_i l_i /le L /qquad /forall i /in I //a_i /ge 0 /qquad /quad /quad /forall i /in I /]
數據帶入模型
以下所有的求解都可以用CPLEX進行求解,直接用CPLEX IDE實現
1. 啟發式獲得初始切割方案
首先有可行的切割方案才能構造出主問題,因此可以用啟發式先計算出一些可行的切割方案,用于構造主問題。很簡單的,每根鋼管只生產一種產品,可以得到三種切割方案
2.開始列生成迭代
第1次迭代
松弛限制主問題:
/[min /quad x_1 + x_2 + x_3 //s.t./qquad/qquad/qquad/qquad/qquad///quad/quad/quad5x_1 /qquad /qquad /quad /ge 25 ///quad/quad/quad/qquad 2x_2 /qquad /quad /ge 20 ///quad/quad/quad/qquad /qquad 2x_3 /quad/ge 18 // /quad/quad/quad x_1,/quad x_2,/quad x_3 /quad /ge 0 /]
對偶問題:
/[max /quad 25 v_1 + 20 v_2 + 18v_3 //s.t./qquad/qquad/qquad/qquad/qquad///qquad /quad 5v_1 /qquad /qquad /qquad /quad/le 1 ///qquad /quad/qquad /quad 2v_2 /qquad /quad /quad/le 1 ///qquad /quad/qquad /qquad /qquad 2v_3/quad /le 1 // /quad/quad /quad v_1,/quad /quad v_2,/quad /quad v_3 /quad /ge 0 /]
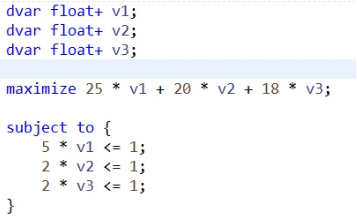

求得對偶變量的值,將其帶入到子問題中
子問題:
/[min /quad 1-0.2a_1-0.5a_2-0.5a_3 //s.t./qquad/qquad/qquad/qquad/qquad///quad/quad/quad 3a_1+6a_2+7a_3 /le 16///quad/quad/quad a_1, /quad a_2, /quad a_3 /quad /ge 0 /]

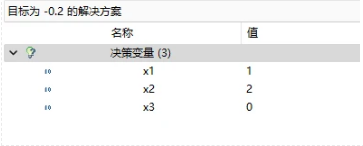
目標函數值為-0.2<0,可以加入到主問題中繼續求解,新加入的一列是/(a_4=[1,2,0]^T/),表示這個方案中一根鋼管切出一根3m和2根6米
第2次迭代
松弛限制主問題:
/[min /quad x_1 + x_2 + x_3 + x_4 //s.t./qquad/qquad/qquad/qquad/qquad///quad/quad/quad5x_1 /qquad /qquad /quad + x_4 /quad/ge 25 ///quad/quad/quad/qquad 2x_2 /qquad /quad + 2x_4 /ge 20 ///quad/quad/quad/qquad /qquad 2x_3 /quad /quad/quad/quad/ge 18 // /quad/quad/quad x_1,/quad x_2,/quad x_3, /quad x_4 /quad /ge 0 /]
對偶問題:
/[max /quad 25 v_1 + 20 v_2 + 18v_3 //s.t./qquad/qquad/qquad/qquad/qquad///qquad /quad 5v_1 /qquad /qquad /qquad /quad/le 1 ///qquad /quad/qquad /quad 2v_2 /qquad /quad /quad/le 1 ///qquad /quad/qquad /qquad /qquad 2v_3/quad /le 1 ///qquad /quad v_1/quad+2v_2 /quad/quad/quad/quad/le 1 // /quad/quad /quad v_1, /qquad v_2, /qquad v_3 /quad /ge 0 /]
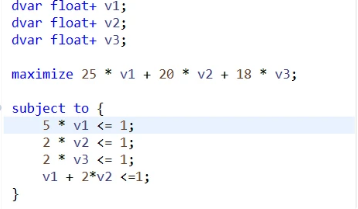
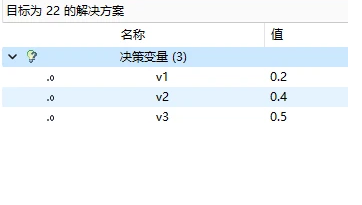
求得對偶變量的值,將其帶入到子問題中
子問題:
/[min /quad 1-0.2a_1-0.4a_2-0.5a_3 //s.t./qquad/qquad/qquad/qquad/qquad///quad/quad/quad 3a_1+6a_2+7a_3 /le 16///quad/quad/quad a_1, /quad a_2, /quad a_3 /quad /ge 0 /]

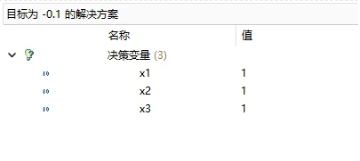
目標函數值為-0.1<0,可以加入到主問題中繼續求解,可以加入到主問題中繼續求解,新加入的一列是/(a_4=[1,1,1]^T/),表示這個方案中一根鋼管切出1根3m,1根6米,1根7米
第3次迭代
松弛限制主問題:
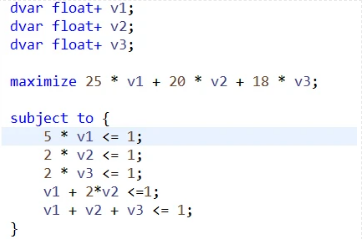
/[min /quad x_1 + x_2 + x_3 + x_4 + x_5//s.t./qquad/qquad/qquad/qquad/qquad///quad/quad/quad5x_1 /qquad /qquad /quad + x_4 /quad + x_5/ge 25 ///quad/quad/quad/qquad 2x_2 /qquad /quad + 2x_4 +x_5/ge 20 ///quad/quad/quad/qquad /qquad 2x_3 /quad /quad/quad/quad +x_5/ge 18 // /quad/quad x_1,/quad x_2,/quad x_3, /quad x_4, /quad x_5 /quad/quad/ge 0 /]
對偶問題:
/[max /quad 25 v_1 + 20 v_2 + 18v_3 //s.t./qquad/qquad/qquad/qquad/qquad///qquad /quad 5v_1 /qquad /qquad /qquad /quad/le 1 ///qquad /quad/qquad /quad 2v_2 /qquad /quad /quad/le 1 ///qquad /quad/qquad /qquad /qquad 2v_3/quad /le 1 ///qquad /quad v_1/quad+2v_2 /quad/quad/quad/quad/le 1 // /qquad /quad v_1/quad+v_2/quad+v_3 /quad/le 1 ///quad/quad /quad v_1, /qquad v_2, /qquad v_3 /quad /ge 0 /]
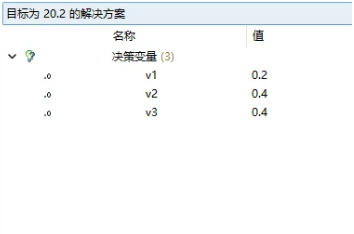
求得對偶變量的值,將其帶入到子問題中
子問題:
/[min /quad 1-0.2a_1-0.4a_2-0.4a_3 //s.t./qquad/qquad/qquad/qquad/qquad///quad/quad/quad 3a_1+6a_2+7a_3 /le 16///quad/quad/quad a_1, /quad a_2, /quad a_3 /quad /ge 0 /]

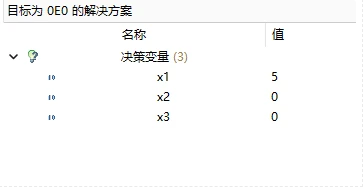
根據求解可以得到
目標值:20.2
切割方案:方案1選擇1.2個;方案4選擇1個,方案5選擇18個
最后求得的結果包含了小數,如果想要取得整數解,需要結合分支定界算法













