資訊專欄INFORMATION COLUMN

小編寫這篇文章的主要目的是,教給大家怎么使用哈夫曼編碼,也就是霍夫曼編碼,并把具體的一些代碼實例給大家貼了出來,希望可以為大家帶來幫助。
一、用C語言實現哈夫曼編碼
1、代碼解釋
(1)建立一個互相連接的表
我們在創建哈夫曼樹的過程之中,要對互相之間的連接點進行增刪查改,所以使用雙向鏈路表格會更加的容易。
'''C
#include <stdlib.h>
#include <stdio.h>
#include <windows.h>
//哈夫曼樹結構體,數據域存儲字符及其權重
typedef struct node
{
char c;
int weight;
struct node *lchild, *rchild;
}Huffman, *Tree;
//雙向鏈表結構體,數據域存儲哈夫曼樹結點
typedef struct list
{
Tree root;
struct list *pre;
struct list *next;
}List, *pList;
//創建雙向鏈表,返回頭結點指針
pList creatList()
{
pList head = (pList)malloc(sizeof(List));
pList temp1 = head;
pList temp2 = (pList)malloc(sizeof(List));
temp1->pre = NULL;
temp1->next = temp2;
temp1->root = (Tree)malloc(sizeof(Huffman));
temp1->root->c = 'a';
temp1->root->weight = 22;
temp1->root->lchild = NULL;
temp1->root->rchild = NULL;
temp2->pre = temp1;
temp1 = temp2;
temp2 = (pList)malloc(sizeof(List));
temp1->next = temp2;
temp1->root = (Tree)malloc(sizeof(Huffman));
temp1->root->c = 'b';
temp1->root->weight = 5;
temp1->root->lchild = NULL;
temp1->root->rchild = NULL;
temp2->pre = temp1;
temp1 = temp2;
temp2 = (pList)malloc(sizeof(List));
temp1->next = temp2;
temp1->root = (Tree)malloc(sizeof(Huffman));
temp1->root->c = 'c';
temp1->root->weight = 38;
temp1->root->lchild = NULL;
temp1->root->rchild = NULL;
temp2->pre = temp1;
temp1 = temp2;
temp2 = (pList)malloc(sizeof(List));
temp1->next = temp2;
temp1->root = (Tree)malloc(sizeof(Huffman));
temp1->root->c = 'd';
temp1->root->weight = 9;
temp1->root->lchild = NULL;
temp1->root->rchild = NULL;
temp2->pre = temp1;
temp1 = temp2;
temp2 = (pList)malloc(sizeof(List));
temp1->next = temp2;
temp1->root = (Tree)malloc(sizeof(Huffman));
temp1->root->c = 'e';
temp1->root->weight = 44;
temp1->root->lchild = NULL;
temp1->root->rchild = NULL;
temp2->pre = temp1;
temp1 = temp2;
temp2 = (pList)malloc(sizeof(List));
temp1->next = temp2;
temp1->root = (Tree)malloc(sizeof(Huffman));
temp1->root->c = 'f';
temp1->root->weight = 12;
temp1->root->lchild = NULL;
temp1->root->rchild = NULL;
temp2->pre = temp1;
temp1 = temp2;
temp1->next = NULL;
temp1->root = (Tree)malloc(sizeof(Huffman));
temp1->root->c = 'g';
temp1->root->weight = 65;
temp1->root->lchild = NULL;
temp1->root->rchild = NULL;
return head;
}(2)建立起棧的結構
解碼過程需要用到兩個棧,一個用來存放樹結點,一個用來存放碼0和1
'''C
#define STACK_INIT_SIZE 100 //棧初始開辟空間大小
#define STACK_INCREMENT 10 //棧追加空間大小
//字符棧結構體,存放編碼'0'和'1'
typedef struct {
char *base;
char *top;
int size;
}charStack;
//棧初始化
charStack charStackInit()
{
charStack s;
s.base = (char *)malloc(sizeof(char)*STACK_INIT_SIZE);
s.top = s.base;
s.size = STACK_INIT_SIZE;
return s;
}
//入棧
void charPush(charStack *s, char e)
{
if(s->top - s->base >= s->size)
{
s->size += STACK_INCREMENT;
s->base = realloc(s->base, sizeof(char)*s->size);
}
*s->top = e;
s->top++;
}
//出棧
char charPop(charStack *s)
{
if(s->top != s->base)
{
s->top--;
return *s->top;
}
return -1;
}
//得到棧頂元素,但不出棧
char charGetTop(charStack *s)
{
s->top--;
char temp = *s->top;
s->top++;
return temp;
}
//棧結構體,存放哈夫曼樹結點
typedef struct
{
Huffman *base;
Huffman *top;
int size;
}BiStack;
//棧初始化
BiStack stackInit()
{
BiStack s;
s.base = (Huffman *)malloc(sizeof(Huffman)*STACK_INIT_SIZE);
s.top = s.base;
s.size =STACK_INIT_SIZE;
return s;
}
//入棧
void push(BiStack *s, Huffman e)
{
if(s->top - s->base >= s->size)
{
s->size += STACK_INCREMENT;
s->base = (Huffman *)realloc(s->base, sizeof(Huffman)*s->size);
}
*s->top = e;
s->top++;
}
//出棧
Huffman pop(BiStack *s)
{
Huffman temp;
s->top--;
temp = *s->top;
return temp;
}
//得到棧頂元素,但不出棧
Huffman getTop(BiStack s)
{
Huffman temp;
s.top--;
temp = *s.top;
return temp;
}
char stack[7][10]; //記錄a~g的編碼
//遍歷棧,得到字符c的編碼
void traverseStack(charStack s, char c)
{
int index = c - 'a';
int i = 0;
while(s.base != s.top)
{
stack[index][i] = *s.base;
i++;
s.base++;
}
}(3)創建哈夫曼樹
'''C
//通過雙向鏈表創建哈夫曼樹,返回根結點指針
Tree creatHuffman(pList head)
{
pList list1 = NULL;
pList list2 = NULL;
pList index = NULL;
Tree root = NULL;
while(head->next != NULL) //鏈表只剩一個結點時循環結束,此結點數據域即為哈夫曼樹的根結點
{
list1 = head;
list2 = head->next;
index = list2->next;
root = (Tree)malloc(sizeof(Huffman));
while(index != NULL) //找到鏈表中權重最小的兩個結點list1,list2
{
if(list1->root->weight > index->root->weight || list2->root->weight > index->root->weight)
{
if(list1->root->weight > list2->root->weight) list1 = index;
else list2 = index;
}
index = index->next;
}
//list1和list2設為新結點的左右孩子
if(list2->root->weight > list1->root->weight)
{
root->lchild = list1->root;
root->rchild = list2->root;
}
else
{
root->lchild = list2->root;
root->rchild = list1->root;
}
//新結點字符統一設為空格,權重設為list1與list2權重之和
root->c = ' ';
root->weight = list1->root->weight + list2->root->weight;
//list1數據域替換成新結點,并刪除list2
list1->root = root;
list2->pre->next = list2->next;
if(list2->next != NULL)
list2->next->pre = list2->pre;
}
return head->root;
}(4)編碼
'''C
char stack[7][10]; //記錄a~g的編碼
//遍歷棧,得到字符c的編碼
void traverseStack(charStack s, char c)
{
int index = c - 'a';
int i = 0;
while(s.base != s.top)
{
stack[index][i] = *s.base;
i++;
s.base++;
}
}
//通過哈夫曼樹編碼
void encodeHuffman(Tree T)
{
BiStack bs = stackInit();
charStack cs = charStackInit();
Huffman root = *T;
Tree temp = NULL;
push(&bs, root); //根結點入棧
while(bs.top != bs.base) //棧空表示遍歷結束
{
root = getTop(bs);
temp = root.lchild; //先訪問左孩子
while(temp != NULL) //左孩子不為空
{
//將結點左孩子設為空,代表已訪問其左孩子
root.lchild = NULL;
pop(&bs);
push(&bs, root);
//左孩子入棧
root = *temp;
temp = root.lchild;
push(&bs, root);
//'0'入字符棧
charPush(&cs, '0');
}
temp = root.rchild; //后訪問右孩子
while(temp == NULL) //右孩子為空,代表左右孩子均已訪問,結點可以出棧
{
//結點出棧
root = pop(&bs);
//尋到葉子結點,可以得到結點中字符的編碼
if(root.c != ' ')
traverseStack(cs, root.c);
charPop(&cs); //字符棧出棧
if(bs.top == bs.base) break; //根結點出棧,遍歷結束
//查看上一級結點是否訪問完左右孩子
root = getTop(bs);
temp = root.rchild;
}
if(bs.top != bs.base)
{
//將結點右孩子設為空,代表已訪問其右孩子
root.rchild = NULL;
pop(&bs);
push(&bs, root);
//右孩子入棧
root = *temp;
push(&bs, root);
//'1'入字符棧
charPush(&cs, '1');
}
}
}(5)解碼
'''C
char stack[7][10]; //記錄a~g的編碼
//遍歷棧,得到字符c的編碼
void traverseStack(charStack s, char c)
{
int index = c - 'a';
int i = 0;
while(s.base != s.top)
{
stack[index][i] = *s.base;
i++;
s.base++;
}
}
//通過哈夫曼樹編碼
void encodeHuffman(Tree T)
{
BiStack bs = stackInit();
charStack cs = charStackInit();
Huffman root = *T;
Tree temp = NULL;
push(&bs, root); //根結點入棧
while(bs.top != bs.base) //棧空表示遍歷結束
{
root = getTop(bs);
temp = root.lchild; //先訪問左孩子
while(temp != NULL) //左孩子不為空
{
//將結點左孩子設為空,代表已訪問其左孩子
root.lchild = NULL;
pop(&bs);
push(&bs, root);
//左孩子入棧
root = *temp;
temp = root.lchild;
push(&bs, root);
//'0'入字符棧
charPush(&cs, '0');
}
temp = root.rchild; //后訪問右孩子
while(temp == NULL) //右孩子為空,代表左右孩子均已訪問,結點可以出棧
{
//結點出棧
root = pop(&bs);
//尋到葉子結點,可以得到結點中字符的編碼
if(root.c != ' ')
traverseStack(cs, root.c);
charPop(&cs); //字符棧出棧
if(bs.top == bs.base) break; //根結點出棧,遍歷結束
//查看上一級結點是否訪問完左右孩子
root = getTop(bs);
temp = root.rchild;
}
if(bs.top != bs.base)
{
//將結點右孩子設為空,代表已訪問其右孩子
root.rchild = NULL;
pop(&bs);
push(&bs, root);
//右孩子入棧
root = *temp;
push(&bs, root);
//'1'入字符棧
charPush(&cs, '1');
}
}
}(6)主函數
'''C
void main()
{
pList pl = creatList();
printf("字符的權重如下\n");
for(pList l = pl; l->next != NULL; l = l->next)
printf("字符%c的權重是 %d\n", l->root->c, l->root->weight);
Tree T = creatHuffman(pl);
encodeHuffman(T);
printf("\n\n字符編碼結果如下\n");
for(int i = 0; i < 7; i++)
printf("%c : %s\n", i+'a', stack[i]);
char code[100];
printf("\n\n請輸入編碼:\n");
scanf("%s", code);
printf("解碼結果如下:\n");
decodeHuffman(T, code);
printf("%s\n", decode);
printf("\n\n");
system("date /T");
system("TIME /T");
system("pause");
exit(0);
}2、運轉答案如下:
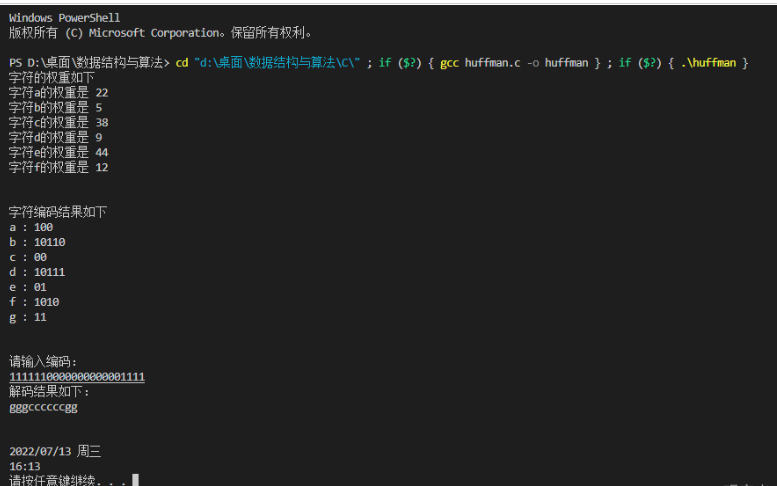
二、實現Python功能
1、代碼解釋
(1)創建哈夫曼樹
#coding=gbk
import datetime
import time
from pip._vendor.distlib.compat import raw_input
#哈夫曼樹結點類
class Huffman:
def __init__(self, c, weight):
self.c = c
self.weight = weight
self.lchild = None
self.rchild = None
#創建結點左右孩子
def creat(self, lchild, rchild):
self.lchild = lchild
self.rchild = rchild
#創建列表
def creatList():
list = []
list.append(Huffman('a', 22))
list.append(Huffman('b', 5))
list.append(Huffman('c', 38))
list.append(Huffman('d', 9))
list.append(Huffman('e', 44))
list.append(Huffman('f', 12))
list.append(Huffman('g', 65))
return list
#通過列表創建哈夫曼樹,返回樹的根結點
def creatHuffman(list):
while len(list) > 1: #列表只剩一個結點時循環結束,此結點即為哈夫曼樹的根結點
i = 0
j = 1
k = 2
while k < len(list): #找到列表中權重最小的兩個結點list1,list2
if list[i].weight > list[k].weight or list[j].weight > list[k].weight:
if list[i].weight > list[j].weight:
i = k
else:
j = k
k += 1
root = Huffman(' ', list[i].weight + list[j].weight) #新結點字符統一設為空格,權重設為list1與list2權重之和
if list[i].weight < list[j].weight: #list1和list2設為新結點的左右孩子
root.creat(list[i], list[j])
else:
root.creat(list[j], list[i])
#list1數據域替換成新結點,并刪除list2
list[i] = root
list.remove(list[j])
return list[0](2)編碼
#通過哈夫曼樹編碼 def encodeHuffman(T): code = [[], [], [], [], [], [], []] #列表實現棧結構 treeStack = [] codeStack = [] treeStack.append(T) while treeStack != []: #棧空代表遍歷結束 root = treeStack[-1] temp = root.lchild while temp != None: #將結點左孩子設為空,代表已訪問其左孩子 root.lchild = None #左孩子入棧 treeStack.append(temp) root = temp temp = root.lchild #0入編碼棧 codeStack.append(0) temp = root.rchild #后訪問右孩子 while temp == None: #右孩子為空,代表左右孩子均已訪問,結點可以出棧 root = treeStack.pop() #結點出棧 #尋到葉子結點,可以得到結點中字符的編碼 if root.c != ' ': codeTemp = codeStack.copy() code[ord(root.c) - 97] = codeTemp if treeStack == []: #根結點出棧,遍歷結束 break codeStack.pop() #編碼棧出棧 #查看上一級結點是否訪問完左右孩子 root = treeStack[-1] temp = root.rchild if treeStack != []: treeStack.append(temp) #右孩子入棧 root.rchild = None #將結點右孩子設為空,代表已訪問其右孩子 codeStack.append(1) #1入編碼棧 return code
(3)解碼
#通過哈夫曼樹解碼 def decodeHuffman(T, strCode): decode = [] index = 0 while index < len(strCode): #01編碼字符串讀完,解碼結束 root = T while root.lchild != None: #找到葉子結點 if index < len(strCode): if strCode[index] == '0': root = root.lchild else: root = root.rchild index += 1 else: break decode.append(root.c) #葉子結點存放的字符即為解碼得到的字符 return decode
(4)主函數
if __name__ == '__main__':
list = creatList()
print("字符的權重如下")
for i in range(len(list)):
print("字符{}的權重為: {}".format(chr(i+97), list[i].weight))
T = creatHuffman(list)
code = encodeHuffman(T)
print("\n字符編碼結果如下")
for i in range(len(code)):
print(chr(i+97), end=' : ')
for j in range(len(code[i])):
print(code[i][j], end='')
print("")
strCode = input("\n請輸入編碼:\n")
#哈夫曼樹在編碼時被破壞,必須重建哈夫曼樹
list = creatList()
T = creatHuffman(list)
decode = decodeHuffman(T, strCode)
print("解碼結果如下:")
for i in range(len(decode)):
print(decode[i], end='')
print("\n\n")
datetime = datetime.datetime.now()
print(datetime.strftime("%Y-%m-%d\n%H:%M:%S"))
input("Press Enter to exit…")2、運行結果
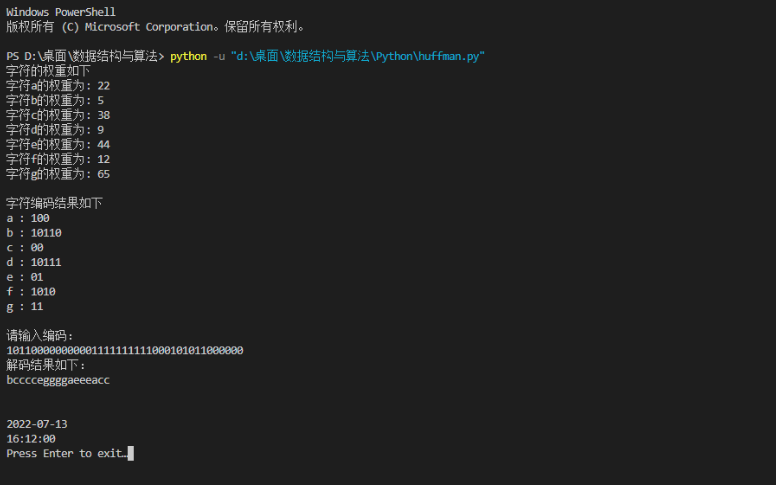
以上就是關于哈夫曼編碼的相關介紹,希望可以為各位讀者帶來一定的幫助。。
文章版權歸作者所有,未經允許請勿轉載,若此文章存在違規行為,您可以聯系管理員刪除。
轉載請注明本文地址:http://m.specialneedsforspecialkids.com/yun/127609.html
摘要:在計算機信息處理中,哈夫曼編碼是一種一致性編碼法又稱熵編碼法,用于數據的無損耗壓縮。構造樹時間復雜度選擇兩個使用頻率較小字符在字符串中出現的次數的結點合并生成出一個樹循環創建哈夫曼樹數組函數刪除數組中的第一個元素,并返回被刪除元素的值。 小草主要博客:http://homeway.me/ 演示網址:http://huffman.sinaapp.com/ 源文件下載地址:http:...
閱讀 919·2023-01-14 11:38
閱讀 891·2023-01-14 11:04
閱讀 750·2023-01-14 10:48
閱讀 2039·2023-01-14 10:34
閱讀 956·2023-01-14 10:24
閱讀 833·2023-01-14 10:18
閱讀 506·2023-01-14 10:09
閱讀 583·2023-01-14 10:02