資訊專欄INFORMATION COLUMN

今天我們一起學習什特殊的二叉樹二叉搜索樹(BSTBinary Search Tree),您也可以叫它二叉排序樹、二叉查找樹。現在我們看看。
二叉搜索樹說說明
二叉搜索樹顧名思義就是樹形叉一樣,現在說特質:
對于任何一個非空節點來說,它左子樹上的值必須小于當前值;
對于任何一個非空節點來說,它右子樹上的值必須大于當前值;
任何一顆子樹滿足上面的條件;
如下圖所示:
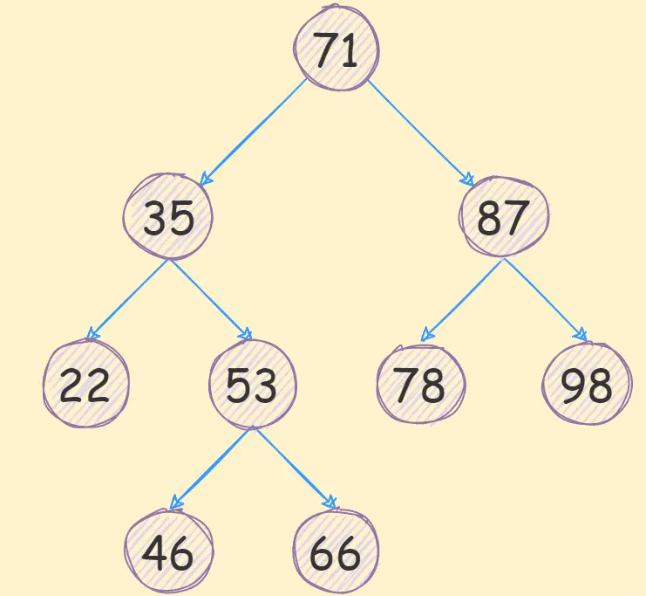
上圖就是一顆二叉搜索樹,總結來說就是右邊數值大于左邊數值。上圖的根節點的值71,它的左子樹的值分別是22、35、46、53和66,這幾個都是滿足左子樹小于當前值;它的右子樹的值分別是78、87和98,這幾個值是滿足右子樹大于當前值的;上述就顯示出二叉搜索樹特質。
根據二叉搜索樹的特質,我們還能得到以下結論:
二叉搜索樹的任何一個節點的左子樹、右子樹都是一顆二叉搜索樹;
二叉搜索樹的最小的節點是整顆樹的最左下角的葉子節點;
二叉搜索樹的最大的節點是整棵樹的最右下角的葉子節點;
構建一顆二叉搜索樹
先項目中用avaScript來實現構建一顆二叉搜索樹,我們可以想象成一個一個節點組成,這里我們就用于class創建一個節點類,
示例代碼如下:
class BinarySearchTree {
constructor() {
// 初始化根節點
this.root = null
}
// 創建一個節點
Node(val) {
return {
left: null, // 左子樹
right: null, // 右子樹
parent: null, // 父節點
val,
}
}
}這里一個節點由四部分組成,分別是指向左子樹的指針、指向右子樹的指針、指向父節點的指針以及當前值。
二叉搜索樹的操作
關于二叉樹的遍歷操作我們在上一篇文章中已經介紹了,這里不在重復,這里主要介紹如下操作:
插入操作
查找操作
刪除操作
向二叉搜索樹中插入數據
向一個二叉搜索樹插入數據實現思路如下:
判斷root是否為空,如果為空則創建root;
如果root非空,則需要判斷插入節點的val比根節點的val是大還是小;
如果比根節點小,說明是左子樹的節點;
如果比根節點大,說明是右子樹的節點;
上面重復執行直至我們找到一個點,當這個點小于我們要插入的值,且不存在右子樹,將這個點作為其右葉子節點;當這個點大于我們要插入的值,且不存在右子樹,將這個點作為其左葉子節點。
示例代碼如下
// 創建要給插入節點的方法
insertNode(val) {
const that = this
// 允許接受一個數組,批量插入
if (Object.prototype.toString.call(val) === '[object Array]') {
val.forEach(function (v) {
that.insertNode(v)
})
return
}
if (typeof val !== 'number') throw Error('插入的值不是一個數字')
const newNode = this.Node(val)
if (this.root) {
// 根節點非空
this.#insertNode(this.root, newNode)
} else {
// 根節點是空的,直接創建
this.root = newNode
}
}
// 私有方法,插入節點
#insertNode(root, newNode) {
if (newNode.val < root.val) {
// 新節點比根節點小,左子樹
if (root.left === null) {
// 如果左子樹上沒有內容,則直接插入,如果有,尋找下一個插入位置
root.left = newNode
root.left.parent = root
} else {
this.#insertNode(root.left, newNode)
}
} else {
// 新節點比根節點大,右子樹
if (root.right === null) {
// 如果右子樹上沒有內容,則直接插入,如果有,尋找下一個插入位置
root.right = newNode
root.right.parent = root
} else {
this.#insertNode(root.right, newNode)
}
}
}在類中定義了insertNode方法,這個方法接受數值或者數值類型的數組,將其插入這個二叉搜索樹中;插入方法我們定義了一個私有的#insertNode方法,用于節點的插入。
現在為實現預估動作結果,在這里定義了一個靜態方法,用于中序遍歷(因為中序遍歷的順序是左根右,在二叉搜索樹中使用中序排序,最終結果是從小到大依次排序的)這個樹,并返回一個數組,
示例代碼如下:
// 中序遍歷這個樹
static inorder(root) {
if (!root) return
const result = []
const stack = []
// 定義一個指針
let p = root
// 如果棧中有數據或者p不是null,則繼續遍歷
while (stack.length || p) {
// 如果p存在則一致將p入棧并移動指針
while (p) {
// 將 p 入棧,并以移動指針
stack.push(p)
p = p.left
}
const node = stack.pop()
result.push(node.val)
p = node.right
}
return result
}測試代碼如下:
const tree = new BinarySearchTree()
tree.insertNode([71, 35, 87, 22, 53, 46, 66, 78, 98])
const arr = BinarySearchTree.inorder(tree.root)
console.log(arr) // [ 22, 35, 46, 53, 66,71, 78, 87, 98 ]
最終的樹結構如下:
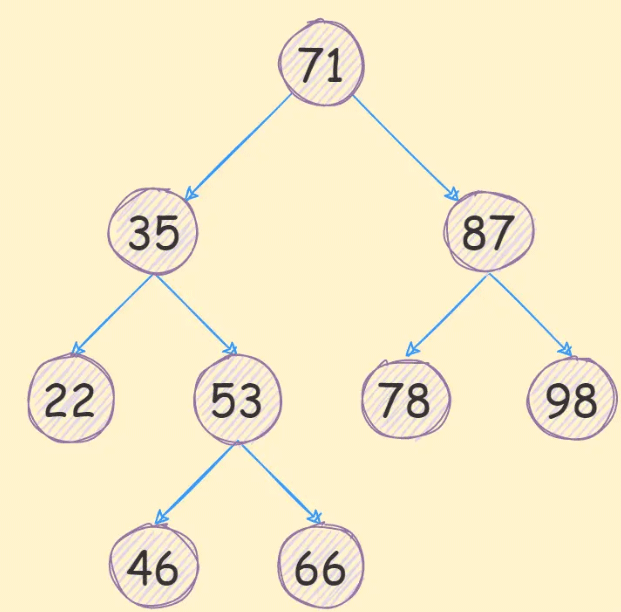
查找二叉搜索樹中的數據
現在我們封裝一個find方法,用于查找二叉搜索樹中的某個數據,假如我們查找66這個數據,利用上面那個樹,
其查找思路如下圖所示:
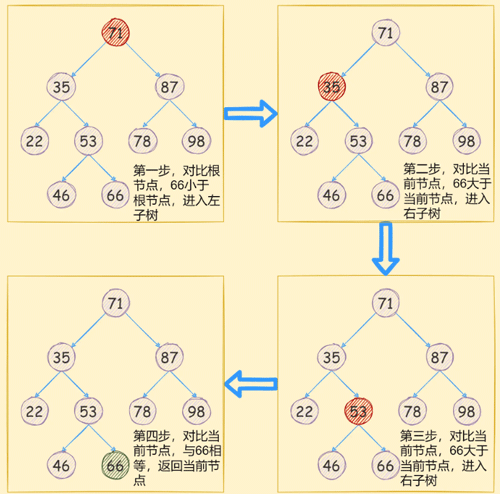
遞歸方式實現如下:
/**
* 根據 val 查找節點
* @param {number} val 需要查找的數值
* @returns 如果找到返回當前節點的引用,如果未找到返回 undefined
*/
find(val) {
if (typeof val !== 'number') throw Error('插入的值不是一個數字')
let node = this.root
while (node) {
if (node.val < val) {
// 進入右子樹
node = node.right
} else if (node.val > val) {
// 進入左子樹
node = node.left
} else {
return node
}
}
return
}兩者相對來說,使用迭代的方式更優一些。
刪除二叉搜索樹的某個節點
前驅后繼節點
在開始刪除二叉搜索樹中的某個節點之前,我們先來了解一下什么是前驅和后繼節點;
前驅節點指的是使用中序遍歷當前二叉搜索樹時,當前節點的上一個節點就是前驅節點,換一種說法就是在二叉搜索樹中,當前節點的左子樹的最大值,就是該節點的前驅節點;
后繼節點指的是使用中序遍歷當前二叉搜索樹時,當前節點的下一個節點就是后繼節點,換一種說法就是在二叉搜索樹中,當前節點的右子樹的最小值,就是該節點的后繼節點;
如下圖所示:
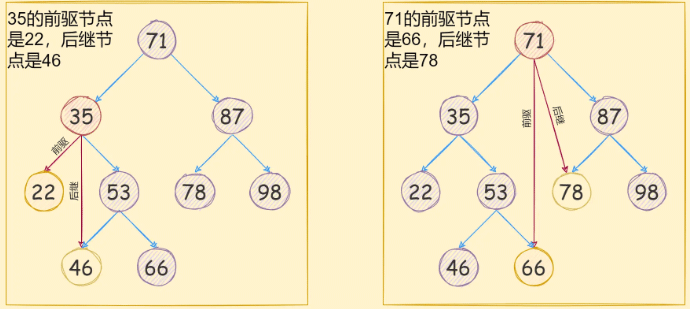
了解了什么是前驅和后繼節點之后,現在我們來開始刪除某個節點。
刪除一個節點的三種情況
當刪除的節點是葉子節點時,只需要將指向它的指針修改為null,即可,如下圖所示:
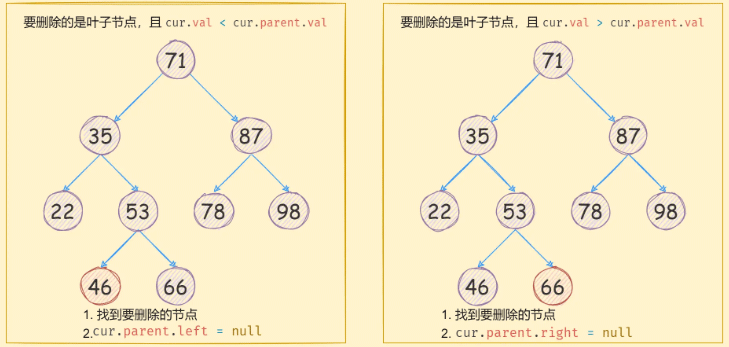
當需要刪除的節點存在一個子節點時,需要將要刪除節點的子節點的parent指針指向要刪除節點的父節點,然后將當前要刪除節點的父節點指向子節點即可,
如下圖所示:
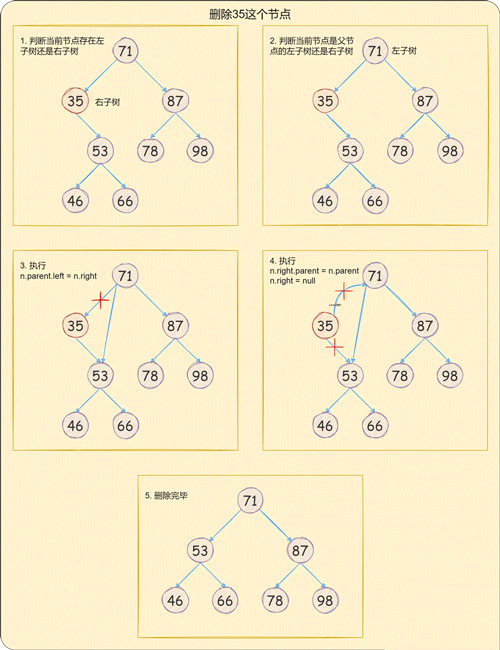
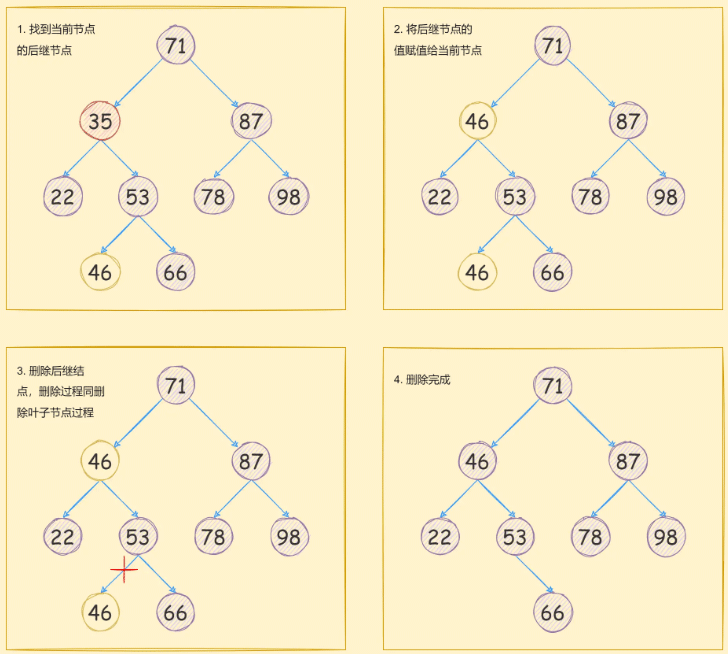
當需要刪除的節點存在一個子節點時, 刪除步驟如下:
找到當前節點的前驅或者后繼節點,這里選擇后繼;
然后將后繼節點的值賦值給當前節點;
刪除后繼節點。
如下圖所示:
現在我們將這些情況已經分析完成了,現在通過代碼實現一下。
實現代碼
實現代碼如下:
remove(val) {
// 1. 刪除節點
const cur = this.find(val)
if (!val) return false // 未找到需要刪除的節點
if (!cur.left && !cur.right) {
// 1. 當前節點是葉子節點的情況
this.#removeLeaf(cur)
} else if (cur.left && cur.right) {
// 2. 當前節點存在兩個子節點
// 2.1 找到當前節點的后繼節點
const successorNode = this.#minNode(cur.right)
// 2.2 將后繼節點的值賦值給當前值
cur.val = successorNode.val
if (!successorNode.left && !successorNode.right) {
// 2.3 后繼節點是葉子節點,直接刪除
this.#removeLeaf(successorNode)
} else {
// 2.4 后繼節點不是葉子節點
// 2.4.1記錄該節點的子節點,
let child =
successorNode.left !== null ? successorNode.left : successorNode.right
// 2.4.2 記錄該節點的父節點
let parent = successorNode.parent
// 2.4.3 如果當前父節點的left是后繼結點,則把后繼結點的父節點的left指向后繼結點的子節點
if (parent.left === successorNode) {
parent.left = child
} else {
// 2.4.4 如果不是,則讓父節點的right指向后繼結點的子節點
parent.right = child
}
// 2.4.5 修改子節點的parent指針
child.parent = parent
}
// 2.3 刪除后繼節點
} else {
// 記錄當前節點的是否是父節點的左子樹
const isLeft = cur.val < cur.parent.val
// 3. 僅存在一個子節點
if (cur.left) {
// 3.1 當前節點存在左子樹
cur.parent[isLeft ? 'left' : 'right'] = cur.left
cur.left.parent = cur.parent
} else if (cur.right) {
// 3.2 當前節點存在右子樹
cur.parent[isLeft ? 'left' : 'right'] = cur.right
cur.right.parent = cur.parent
}
}
}
// 刪除葉子節點
#removeLeaf(node) {
if (!node) return
const parent = node.parent
if (node.val < parent.val) {
// 當前要刪除的葉子節點是左節點
parent.left = null
} else {
// 當前要刪除的葉子節點是右節點
parent.right = null
}
}
// 查找最小值
#minNode(node) {
if (!node) return
if (!node.left) return node
let p = node.left
while (p.left) {
p = p.left
}
return p
}完整代碼
本篇文章中的完整代碼如下:
class BinarySearchTree {
constructor() {
// 初始化根節點
this.root = null
}
// 創建一個節點
Node(val) {
return {
left: null, // 左子樹
right: null, // 右子樹
parent: null, // 父節點
val,
}
}
/**
* 創建要給插入節點的方法
* @param {number | array[number]} val
* @returns
*/
insertNode(val) {
const that = this
// 允許接受一個數組,批量插入
if (Object.prototype.toString.call(val) === '[object Array]') {
val.forEach(function (v) {
that.insertNode(v)
})
return
}
if (typeof val !== 'number') throw Error('插入的值不是一個數字')
const newNode = this.Node(val)
if (this.root) {
// 根節點非空
this.#insertNode(this.root, newNode)
} else {
// 根節點是空的,直接創建
this.root = newNode
}
}
/**
* 私有方法,插入節點
* @param {Object{Node}} root
* @param {Object{Node}} newNode
*/
#insertNode(root, newNode) {
if (newNode.val < root.val) {
// 新節點比根節點小,左子樹
if (root.left === null) {
// 如果左子樹上沒有內容,則直接插入,如果有,尋找下一個插入位置
root.left = newNode
root.left.parent = root
} else {
this.#insertNode(root.left, newNode)
}
} else {
// 新節點比根節點大,右子樹
if (root.right === null) {
root.right = newNode
root.right.parent = root
} else {
this.#insertNode(root.right, newNode)
}
}
}
/**
* 根據 val 查找節點
* @param {number} val 需要查找的數值
* @returns 如果找到返回當前節點的引用,如果未找到返回 undefined
*/
find(val) {
if (typeof val !== 'number') throw Error('插入的值不是一個數字')
let node = this.root
while (node) {
if (node.val < val) {
// 進入右子樹
node = node.right
} else if (node.val > val) {
// 進入左子樹
node = node.left
} else {
return node
}
}
return
}
// /**
// * 根據 val 查找節點 遞歸版
// * @param {number} val 需要查找的數值
// * @returns 如果找到返回當前節點的引用,如果未找到返回 undefined
// */
// find(val) {
// if (typeof val !== 'number') throw Error('插入的值不是一個數字')
// function r(node, val) {
// // console.log(node)
// if (!node) return
// if (node.val < val) {
// return r(node.right, val)
// } else if (node.val > val) {
// return r(node.left, val)
// } else {
// return node
// }
// }
// return r(this.root, val)
// }
remove(val) {
// 1. 刪除節點
const cur = this.find(val)
if (!val) return false // 未找到需要刪除的節點
if (!cur.left && !cur.right) {
// 1. 當前節點是葉子節點的情況
this.#removeLeaf(cur)
} else if (cur.left && cur.right) {
// 2. 當前節點存在兩個子節點
// 2.1 找到當前節點的后繼節點
const successorNode = this.#minNode(cur.right)
// 2.2 將后繼節點的值賦值給當前值
cur.val = successorNode.val
if (!successorNode.left && !successorNode.right) {
// 2.3 后繼節點是葉子節點,直接刪除
this.#removeLeaf(successorNode)
} else {
// 2.4 后繼節點不是葉子節點
// 2.4.1記錄該節點的子節點,
let child =
successorNode.left !== null ? successorNode.left : successorNode.right
// 2.4.2 記錄該節點的父節點
let parent = successorNode.parent
// 2.4.3 如果當前父節點的left是后繼結點,則把后繼結點的父節點的left指向后繼結點的子節點
if (parent.left === successorNode) {
parent.left = child
} else {
// 2.4.4 如果不是,則讓父節點的right指向后繼結點的子節點
parent.right = child
}
// 2.4.5 修改子節點的parent指針
child.parent = parent
}
// 2.3 刪除后繼節點
} else {
// 記錄當前節點的是否是父節點的左子樹
const isLeft = cur.val < cur.parent.val
// 3. 僅存在一個子節點
if (cur.left) {
// 3.1 當前節點存在左子樹
cur.parent[isLeft ? 'left' : 'right'] = cur.left
cur.left.parent = cur.parent
} else if (cur.right) {
// 3.2 當前節點存在右子樹
cur.parent[isLeft ? 'left' : 'right'] = cur.right
cur.right.parent = cur.parent
}
}
}
// 刪除葉子節點
#removeLeaf(node) {
if (!node) return
const parent = node.parent
if (node.val < parent.val) {
// 當前要刪除的葉子節點是左節點
parent.left = null
} else {
// 當前要刪除的葉子節點是右節點
parent.right = null
}
}
// 查找最小值
#minNode(node) {
if (!node) return
if (!node.left) return node
let p = node.left
while (p.left) {
p = p.left
}
return p
}
// 中序遍歷這個樹
static inorder(root) {
if (!root) return
const result = []
const stack = []
// 定義一個指針
let p = root
// 如果棧中有數據或者p不是null,則繼續遍歷
while (stack.length || p) {
// 如果p存在則一致將p入棧并移動指針
while (p) {
// 將 p 入棧,并以移動指針
stack.push(p)
p = p.left
}
const node = stack.pop()
result.push(node.val)
p = node.right
}
return result
}
}
const tree = new BinarySearchTree()
tree.insertNode([71, 35, 84, 22, 53, 46, 66, 81, 83, 82, 88, 98])
console.log(BinarySearchTree.inorder(tree.root)) // [ 22, 35, 46, 53, 66, 71, 81, 82, 83, 84, 88, 98 ]
tree.remove(71
console.log(BinarySearchTree.inorder(tree.root)) // [ 22, 35, 46, 53, 66, 81, 82, 83, 84, 88, 98 ]總結
此篇結束,大家可以更多深入了解關于二叉搜索樹的其他內容。
文章版權歸作者所有,未經允許請勿轉載,若此文章存在違規行為,您可以聯系管理員刪除。
轉載請注明本文地址:http://m.specialneedsforspecialkids.com/yun/127769.html
摘要:筆者作為一位,將工作以來用到的各種優秀資料神器及框架整理在此,畢竟好記性不如爛鍵盤,此前端知識點大百科全書前端掘金,,不定期更新技巧前端掘金技巧,偶爾更新。計算數組的極值技巧使你的更加專業前端掘金一個幫你提升技巧的收藏集。 CSS 樣式畫各種圖形 - 前端 - 掘金下面是一些我在 CSS 中經常用到的圖案,還有一些是在css-tricks看到的。記錄一下,以后會用到。會持續更新… 一、...
摘要:筆者作為一位,將工作以來用到的各種優秀資料神器及框架整理在此,畢竟好記性不如爛鍵盤,此前端知識點大百科全書前端掘金,,不定期更新技巧前端掘金技巧,偶爾更新。計算數組的極值技巧使你的更加專業前端掘金一個幫你提升技巧的收藏集。 CSS 樣式畫各種圖形 - 前端 - 掘金下面是一些我在 CSS 中經常用到的圖案,還有一些是在css-tricks看到的。記錄一下,以后會用到。會持續更新… 一、...
摘要:每個節點都必須滿足這個屬性,這就是二叉搜索樹。自平衡二叉樹自平衡二叉搜索樹或高度平衡二叉搜索樹是一種特殊類型的二叉搜索樹,它試圖通過自動調整來盡量保持樹的高度或層次盡可能小。自平衡或高度平衡二叉搜索樹有不同的實現。 理解和實現樹 迄今為止,我們對數據結構的探索僅觸及線性部分。無論我們使用數組、鏈表、棧還是隊列,都是線性數據結構。我們已經看到了線性數據結構操作的復雜性,大多數時候,插入和...
摘要:每個列表中的數據項稱為元素。棧被稱為一種后入先出,的數據結構。散列使用的數據結構叫做散列表。不包含任何成員的集合稱為空集,全集則是包含一切可能成員的集合。因此二叉搜索樹需要平衡,即左右子樹高度要相近。 樓樓非計算機專業,但是對計算機也還算喜歡。個人理解若有偏差,歡迎各位批評指正! 對于數據結構和算法一直是我的薄弱環節,相信大多數前端工程師可能多少會有些這方面的弱點,加上數據結構和算法本...
閱讀 570·2023-03-27 18:33
閱讀 760·2023-03-26 17:27
閱讀 658·2023-03-26 17:14
閱讀 611·2023-03-17 21:13
閱讀 545·2023-03-17 08:28
閱讀 1833·2023-02-27 22:32
閱讀 1329·2023-02-27 22:27
閱讀 2211·2023-01-20 08:28