資訊專欄INFORMATION COLUMN

本文關鍵闡述了Python完成1個全連接層的神經元網絡,文章內容緊扣主題進行詳盡的基本介紹,具有很強的實用價值,必須的朋友可以學習一下
序言
在本文中,提前準備用Python重新開始完成1個全連接層的神經元網絡。你可能會說,為何需要自己去完成,有許多庫和架構能夠給我們做這些事,例如Tensorflow、Pytorch等。這兒只想說僅有自己親自完成了,就是自己的。
想起今日他從接觸到了從事神經元網絡有關工作早已是多少2、3年多,在其中也試著用tensorflow或pytorch架構去完成某些傳統互聯網。但是對于反向傳播身后體制還是挺模糊不清。
梯度方向
梯度方向是函數公式升高更快方位,速度最快的方位換句話說正確的方向函數公式樣子很險峻,那樣都是函數公式減少速度最快的方位。
盡管有關某些基礎理論、梯度消失和節點飽和狀態能夠傷害1個1、2、3可是細究或是沒有自信,當然沒有親自動手去完成過個反向傳播和完善練習全過程。所以覺得或是浮于表層,學有所用而。
最近這幾天有段空余時間、因此運用這一段休息日即將把這一部分知識總結一下下、全面了解掌握
大家可能很多人都清楚訓練神經網絡的一個過程,便是升級網絡參數,升級更新的趨勢是減少交叉熵值。其實就是將學習上的問題變換因為一個改善的難題。我們該如何升級主要參數呢?我們應該測算參加練習主要參數相較于損害函數的導數,接著求得梯度方向,接著應用梯度下降法來升級主要參數,迭代更新這一過程,都可以找到1個最好解決方案來降到最低交叉熵。
我們都知道反向傳播關鍵是用來清算交叉熵相較于權重值和參考點的導函數
或許已經聽見或讀到了,一些關于在互聯網根據反向傳播來傳送誤差的信息內容。再根據神經細胞的w和b對誤差成就的尺寸。其實就是將誤差安排到每個神經細胞上。但是這里的誤差(error)是什么意思呀?這一誤差的準確的界定到底是什么呢?答案就是這種誤差是通過每層神經元網絡所成就的,并且某一層樓誤差是后續層誤差前提下平攤的,網絡里第層誤差用以表明。
反向傳播都是基于4個基本方程的,通過這個方程式來數據誤差和交叉熵,這兒把這4個方程式一一列舉
對于如何講解這一4個方程式,接著想要1期共享來闡述。
classNeuralNetwork(object): def__init__(self): pass defforward(self,x): #回到前向傳播的Z可能就是w和b特征函數,鍵入激活函數前的值 #回到激活函數傷害值A #z_s,a_s pass defbackward(self,y,z_s,a_s): #回到前向傳播中學到參數導函數dwdb pass deftrain(self,x,y,batch_size=10,epochs=100,lr=0.001): pass
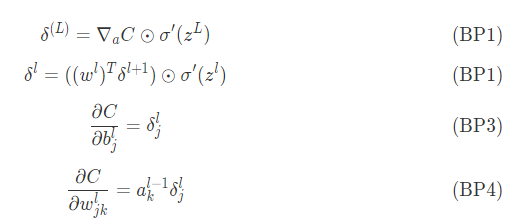
我們是神經網絡學習全過程,其實就是練習全過程。主要分兩階段前向傳播和后向傳播
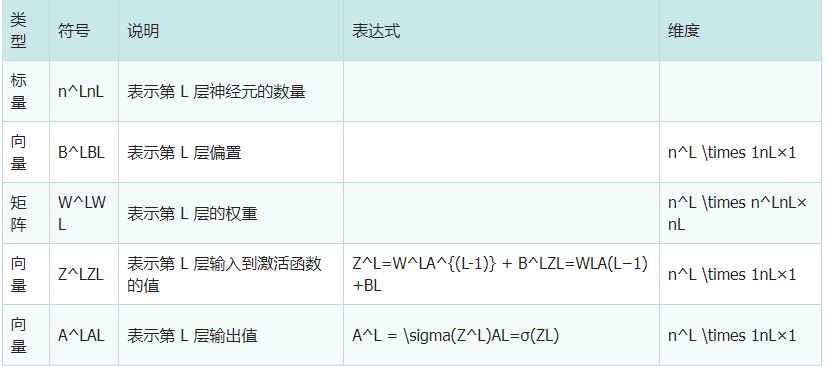
在前向傳播函數中,關鍵測算傳遞的Z和A,有關Z和A指的是什么請參閱前邊報表
在反向傳播中測算可學習培訓自變量w和b的導函數
def__init__(self,layers=[2,10,1],activations=['sigmoid','sigmoid']): assert(len(layers)==len(activations)+1) self.layers=layers self.activations=activations self.weights=[] self.biases=[] foriinrange(len(layers)-1): self.weights.append(np.random.randn(layers[i+1],layers)) self.biases.append(np.random.randn(layers[i+1],1))
layers主要參數用以特定每層神經細胞的數量
activations為每層特定激活函數,其實就是
來簡易解悉一下下編碼assert(len(layers)==len(activations)+1)
foriinrange(len(layers)-1): self.weights.append(np.random.randn(layers[i+1],layers)) self.biases.append(np.random.randn(layers[i+1],1)) 因為權重值連接每個層神經細胞的w和b,可能就兩兩層之間的方程式,上面編碼是對 前向傳播 deffeedforward(self,x): #回到前向傳播的值 a=np.copy(x) z_s=[] a_s=[a] foriinrange(len(self.weights)): activation_function=self.getActivationFunction(self.activations) z_s.append(self.weights.dot(a)+self.biases) a=activation_function(z_s[-1]) a_s.append(a) return(z_s,a_s)
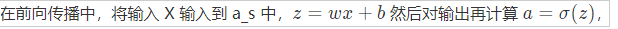
這里激活函數,這個函數返回值是一個函數,在python用lambda來返回一個函數,這里簡答留下一個伏筆,隨后會對其進行修改。
staticmethod
def getActivationFunction(name):
if(name=='sigmoid'):
return lambda x:np.exp(x)/(1+np.exp(x))
elif(name=='linear'):
return lambda x:x
elif(name=='relu'):
def relu(x):
y=np.copy(x)
y[y<0]=0
return y
return relu
else:
print('Unknown activation function.linear is used')
return lambda x:x
[staticmethod]
def getDerivitiveActivationFunction(name):
if(name=='sigmoid'):
sig=lambda x:np.exp(x)/(1+np.exp(x))
return lambda x:sig(x)*(1-sig(x))
elif(name=='linear'):
return lambda x:1
elif(name=='relu'):
def relu_diff(x):
y=np.copy(x)
y[y>=0]=1
y[y<0]=0
return y
return relu_diff
else:
print('Unknown activation function.linear is used')
return lambda x:1
反向傳播
這是本次分享重點
def backpropagation(self,y,z_s,a_s): dw=[]#dC/dW db=[]#dC/dB deltas=[None]*len(self.weights)#delta=dC/dZ計算每一層的誤差 #最后一層誤差 deltas[-1]=((y-a_s[-1])*(self.getDerivitiveActivationFunction(self.activations[-1]))(z_s[-1])) #反向傳播 for i in reversed(range(len(deltas)-1)): deltas<i>=self.weights[i+1].T.dot(deltas[i+1])*(self.getDerivitiveActivationFunction(self.activations<i>)(z_s<i>)) #a=[print(d.shape)for d in deltas] batch_size=y.shape[1] db=[d.dot(np.ones((batch_size,1)))/float(batch_size)for d in deltas] dw=[d.dot(a_s<i>.T)/float(batch_size)for i,d in enumerate(deltas)] #返回權重(weight)矩陣and偏置向量(biases) return dw,db
綜上所述,這篇文章就給大家介紹到這里了,希望可以給大家帶來一定的幫助。
文章版權歸作者所有,未經允許請勿轉載,若此文章存在違規行為,您可以聯系管理員刪除。
轉載請注明本文地址:http://m.specialneedsforspecialkids.com/yun/128844.html
摘要:神經網絡的補充前篇后篇數據預處理權重初始化經典神經網絡搞明白后,我們接下來看看他的變種,也是本系列的主角卷積神經網絡。卷積神經網絡一個普通的卷積神經網絡由各種層按順序堆疊而成,這些層主要分三類卷積層池化層和全連接層。 【DL-CV】神經網絡的補充【DL-CV】數據預處理&權重初始化 經典神經網絡搞明白后,我們接下來看看他的變種,也是本系列的主角——卷積神經網絡(Convolution...
摘要:神經網絡的補充前篇后篇數據預處理權重初始化經典神經網絡搞明白后,我們接下來看看他的變種,也是本系列的主角卷積神經網絡。卷積神經網絡一個普通的卷積神經網絡由各種層按順序堆疊而成,這些層主要分三類卷積層池化層和全連接層。 【DL-CV】神經網絡的補充【DL-CV】數據預處理&權重初始化 經典神經網絡搞明白后,我們接下來看看他的變種,也是本系列的主角——卷積神經網絡(Convolution...
摘要:本論文將嘗試概述卷積網絡的架構,并解釋包含激活函數損失函數前向傳播和反向傳播的數學推導。本文試圖只考慮帶有梯度下降優化的典型卷積神經網絡架構的制定。 近日南洋理工大學研究者發布了一篇描述卷積網絡數學原理的論文,該論文從數學的角度闡述整個卷積網絡的運算與傳播過程。該論文對理解卷積網絡的數學本質非常有幫助,有助于讀者「徒手」(不使用卷積API)實現卷積網絡。論文地址:https://arxiv....
閱讀 919·2023-01-14 11:38
閱讀 891·2023-01-14 11:04
閱讀 750·2023-01-14 10:48
閱讀 2039·2023-01-14 10:34
閱讀 956·2023-01-14 10:24
閱讀 834·2023-01-14 10:18
閱讀 506·2023-01-14 10:09
閱讀 583·2023-01-14 10:02