資訊專欄INFORMATION COLUMN

摘要:前饋網絡的反向傳播從最后的誤差開始,經每個隱藏層的輸出權重和輸入反向移動,將一定比例的誤差分配給每個權重,方法是計算權重與誤差的偏導數,即兩者變化速度的比例。隨后,梯度下降的學習算法會用這些偏導數對權重進行上下調整以減少誤差。
目錄
前饋網絡
遞歸網絡
沿時間反向傳播
梯度消失與梯度膨脹
長短期記憶單元(LSTM)
涵蓋多種時間尺度
本文旨在幫助神經網絡學習者了解遞歸網絡的運作方式,以及一種主要的遞歸網絡,即LSTM的功能和結構。
遞歸網絡是一類人工神經網絡,用于識別諸如文本、基因組、手寫字跡、語音等序列數據的模式,或用于識別傳感器、股票市場、政府機構產生的數值型時間序列數據。
遞歸網絡可以說是最強大的神經網絡,甚至可以將圖像分解為一系列圖像塊,作為序列加以處理。
由于遞歸網絡擁有一種特定的記憶模式,而記憶也是人類的基本能力之一,所以下文會時常將遞歸網絡與人腦的記憶活動進行類比(注 1)。
前饋網絡回顧
要理解遞歸網絡,首先需要了解前饋網絡的基礎知識。這兩種網絡的名字都來自于它們通過一系列網絡節點數學運算來傳遞信息的方式。前饋網絡將信息徑直向前遞送(從不返回已經過的節點),而遞歸網絡則將信息循環傳遞。
在前饋網絡中,樣例輸入網絡后被轉換為一項輸出;在進行有監督學習時,輸出為一個標簽。也就是說,前饋網絡將原始數據映射到類別,識別出信號的模式,例如一張輸入圖像應當給予“貓”還是“大象”的標簽。
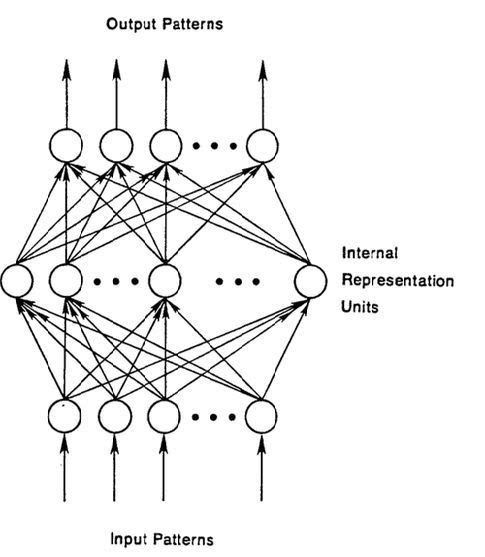
我們用帶有標簽的圖像定型一個前饋網絡,直到網絡在猜測圖像類別時的錯誤達到最少。將參數,即權重定型后,網絡就可以對從未見過的數據進行分類。已定型的前饋網絡可以接受任何隨機的圖片組合,而輸入的第一張照片并不會影響網絡對第二張照片的分類。看到一張貓的照片不會導致網絡預期下一張照片是大象。
這是因為網絡并沒有時間順序的概念,它所考慮的輸入是當前所接受的樣例。前饋網絡仿佛患有短期失憶癥;它們只有早先被定型時的記憶。
遞歸網絡
遞歸網絡與前饋網絡不同,其輸入不僅包括當前所見的輸入樣例,還包括網絡在上一個時刻所感知到信息。以下是[由Elman提出的早期遞歸網絡]的示意圖(https://web.stanford.edu/group/pdplab/pdphandbook/handbookch8.html),圖中最下行的BTSXPE代表當前的輸入樣例,而CONTEXT UNIT則表示前一時刻的輸出。
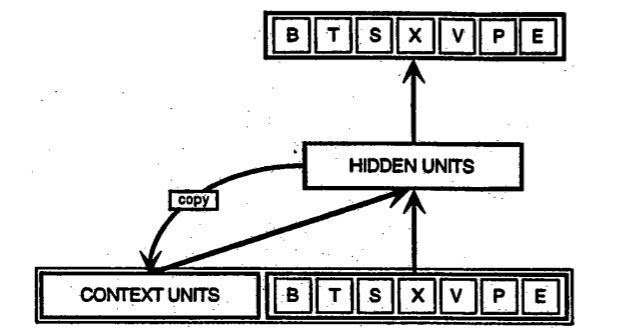
遞歸網絡在第t-1個時間步的判定會影響其在隨后第t個時間步的判定。所以遞歸網絡有來自當下和不久之前的兩種輸入,此二者的結合決定了網絡對于新數據如何反應,與人類日常生活中的情形頗為相似。
遞歸網絡與前饋網絡的區別便在于這種不斷將自身上一刻輸出當作輸入的反饋循環。人們常說遞歸網絡是有記憶的。2 為神經網絡添加記憶的目的在于:序列本身即帶有信息,而遞歸網絡能利用這種信息完成前饋網絡無法完成的任務。
這些順序信息保存在遞歸網絡隱藏狀態中,不斷向前層層傳遞,跨越許多個時間步,影響每一個新樣例的處理。
人類記憶會在體內不斷進行不可見的循環,對我們的行為產生影響而不顯現出完整樣貌,而信息也同樣會在遞歸網絡的隱藏狀態中循環。英語中有許多描述記憶反饋循環的說法。例如,我們會說“一個人被往日所為之事糾纏”,這其實就是在講過去的輸出對當前造成了影響。法國人稱之為“Le passé qui ne passe pas”,即“過去之事不曾過去”。
讓我們用數學語言來描述將記憶向前傳遞的過程:
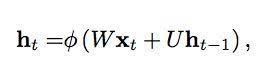
第t個時間步的隱藏狀態是h_t。它是同一時間步的輸入x_t的函數,由一個權重矩陣W(和我們在前饋網絡中使用的一樣)修正,加上前一時間步的隱藏狀態h_t-1乘以它自己的隱藏狀態-隱藏狀態矩陣的U(或稱過渡矩陣,與馬爾可夫鏈近似)。權重矩陣是決定賦予當前輸入及過去隱藏狀態多少重要性的篩選器。它們所產生的誤差將會通過反向傳播返回,用于調整權重,直到誤差不能再降低為止。
權重輸入與隱藏狀態之和用函數??進行擠壓-可能是邏輯S形函數(sigmoid函數)或雙曲正切函數,視具體情況而定-這是將很大或很小的值壓縮至一個邏輯空間內的標準工具,同時也用于產生反向傳播所能接受的梯度。
由于這一反饋循環會在系列的每一個時間步發生,每一個隱藏狀態不僅僅跟蹤前一個隱藏狀態,還包括了記憶能力范圍內所有在h_t-1之前的狀態。
若輸入一系列字母,則遞歸網絡必定會根據第一個字符來決定對第二個字符的感知, 例如,第一個字母如果是q,網絡就可能推斷下一個字母是u,而第一個字母如果是t,則網絡可能推斷下一個字母是h。
由于遞歸網絡具有時間維度,所以可能用動畫示意更為清楚(最先出現的節點垂直線可被視為一個前饋網絡,隨時間展開后變為遞歸網絡)。
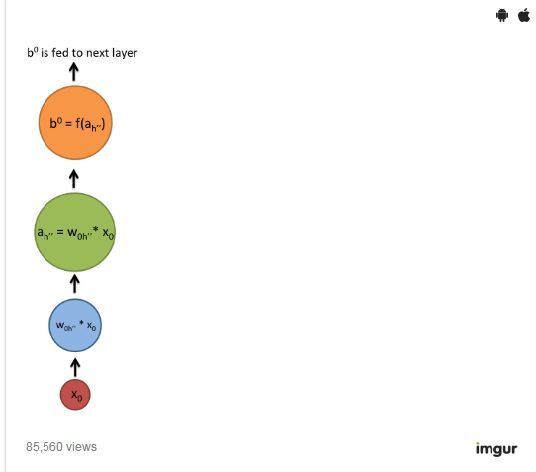
在上圖中,每一個x都是一個輸入樣例,w是用于篩選輸入的權重,a是隱藏層的激活狀態(附加權重后的輸入與上一個隱藏狀態之和),而b則是隱藏層在轉換,或稱“擠壓”后的輸出,使用線性修正或sigmoid單位。
沿時間反向傳播(BPTT)
前文提到,遞歸網絡的目的是準確地對序列輸入進行分類。我們依靠誤差反向傳播和梯度下降來達成這一目標。
前饋網絡的反向傳播從最后的誤差開始,經每個隱藏層的輸出、權重和輸入反向移動,將一定比例的誤差分配給每個權重,方法是計算權重與誤差的偏導數-a??E/a??w,即兩者變化速度的比例。隨后,梯度下降的學習算法會用這些偏導數對權重進行上下調整以減少誤差。
遞歸網絡則使用反向傳播的一種擴展方法,名為沿時間反向傳播,或稱BPTT。在這里,時間其實就表示為一系列定義完備的有序計算,將時間步依次連接,而這些計算就是反向傳播的全部內容。
無論遞歸與否,神經網絡其實都只是形如f(g(h(x)))的嵌套復合函數。增加時間要素僅僅是擴展了函數系列,我們用鏈式法則計算這些函數的導數。
截斷式BPTT
截斷式BPTT 是完整BPTT的近似方法,也是處理較長序列時的優先選擇,因為時間步數量較多時,完整BPTT每次參數更新的正向/反向運算量會變的非常高。該方法的缺點是,由于截斷操作,梯度反向移動的距離有限,因此網絡能夠學習的依賴長度要短于完整的BPTT。
梯度消失(與膨脹)
像大多數神經網絡一樣,遞歸網絡并非新事物。在上世紀九十年代早期,梯度消失問題成為影響遞歸網絡表現的重大障礙。
正如直線表示x如何隨著y的變化而改變,梯度表示所有權重隨誤差變化而發生的改變。如果梯度未知,則無法朝減少誤差的方向調整權重,網絡就會停止學習。
遞歸網絡在尋找最終輸出與許多時間步以前的事件之間的聯系時遇到了重大障礙,因為很難判斷應當為遠距離的輸入賦予多少重要性。(這些輸入就像曾曾…曾祖父母一樣,不斷向前追溯時會迅速增多,而留下的印象通常很模糊。)
原因之一是, 神經網絡中流動的信息會經過許多級的乘法運算。
凡是學過復合利率的人都知道,任何數值,只要頻繁乘以略大于一的數,就會增大到無法衡量的地步(經濟學中的網絡效應和難以避免的社會不平等背后正是這一簡單的數學真理)。反之亦然:將一個數反復乘以小于一的數,也就會有相反的效果。賭徒要是每下一美元注都輸掉97美分,那片刻就會傾家蕩產。
由于深度神經網絡的層和時間步通過乘法彼此聯系,導數有可能消失或膨脹。
梯度膨脹時,每個權重就仿佛是一只諺語中提到的蝴蝶,所有的蝴蝶一齊扇動翅膀,就會在遙遠的地方引發一場颶風。這些權重的梯度增大至飽和,亦即它們的重要性被設得過高。但梯度膨脹的問題相對比較容易解決,因為可以將其截斷或擠壓。而消失的梯度則有可能變得過小,以至于計算機無法處理,網絡無法學習-這個問題更難解決。
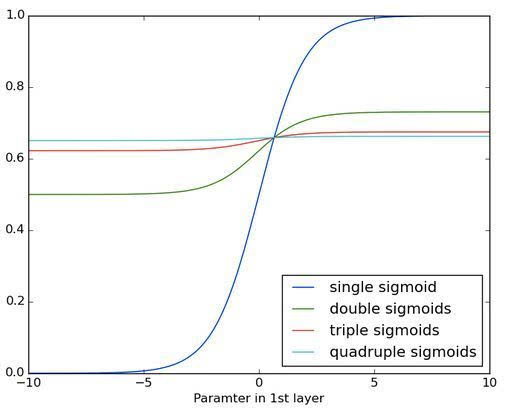
反復應用sigmoid函數的結果如下圖所示。數據曲線越來越平緩,直至在較長的距離上無法檢測到斜度。梯度在經過許多個層后消失的情況與此相似。
長短期記憶單元(LSTM)
九十年代中期,德國學者Sepp Hochreiter和Juergen Schmidhuber提出了遞歸網絡的一種變體,帶有所謂長短期記憶單元,或稱LSTM,可以解決梯度消失的問題。
LSTM可保留誤差,用于沿時間和層進行反向傳遞。LSTM將誤差保持在更為恒定的水平,讓遞歸網絡能夠進行許多個時間步的學習(超過1000個時間步),從而打開了建立遠距離因果聯系的通道。
LSTM將信息存放在遞歸網絡正常信息流之外的門控單元中。這些單元可以存儲、寫入或讀取信息,就像計算機內存中的數據一樣。單元通過門的開關判定存儲哪些信息,以及何時允許讀取、寫入或清除信息。但與計算機中的數字式存儲器不同的是,這些門是模擬的,包含輸出范圍全部在0~1之間的sigmoid函數的逐元素相乘操作。相比數字式存儲,模擬值的優點是可微分,因此適合反向傳播。
這些門依據接收到的信號而開關,而且與神經網絡的節點類似,它們會用自有的權重集對信息進行篩選,根據其強度和導入內容決定是否允許信息通過。這些權重就像調制輸入和隱藏狀態的權重一樣,會通過遞歸網絡的學習過程進行調整。也就是說,記憶單元會通過猜測、誤差反向傳播、用梯度下降調整權重的迭代過程學習何時允許數據進入、離開或被刪除。
下圖顯示了數據在記憶單元中如何流動,以及單元中的門如何控制數據流動。

上圖中的內容很多,如果讀者剛開始學習LSTM,別急著向下閱讀-請先花一些時間思考一下這張圖。只要幾分鐘,你就會明白其中的秘密。
首先,最底部的三個箭頭表示信息從多個點流入記憶單元。當前輸入與過去的單元狀態不只被送入記憶單元本身,同時也進入單元的三個門,而這些門將決定如何處理輸入。
圖中的黑點即是門,分別決定何時允許新輸入進入,何時清除當前的單元狀態,以及/或何時讓單元狀態對當前時間步的網絡輸出產生影響。S_c是記憶單元的當前狀態,而g_y_in是當前的輸入。記住,每個門都可開可關,而且門在每個時間步都會重新組合開關狀態。記憶單元在每個時間步都可以決定是否遺忘其狀態,是否允許寫入,是否允許讀取,相應的信息流如圖所示。
圖中較大的黑體字母即是每項操作的結果。
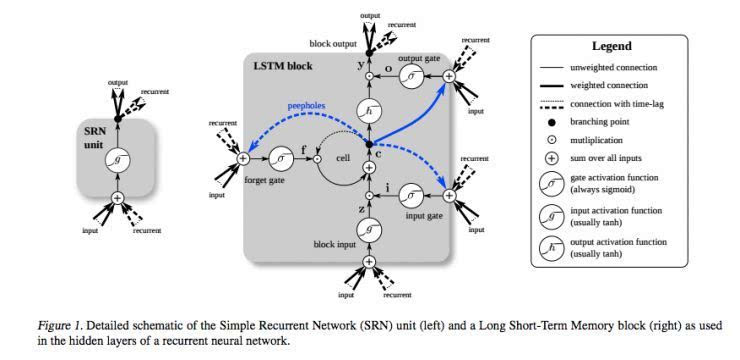
下面是另一張圖,將簡單遞歸網絡(左)與LSTM單元(右)進行對比。藍線可忽略;圖例有助理解。
應當注意的是,LSTM的記憶單元在輸入轉換中給予加法和乘法不同的角色。兩張圖中央的加號其實就是LSTM的秘密。雖然看起來異常簡單,這一基本的改變能幫助LSTM在必須進行深度反向傳播時維持恒定的誤差。LSTM確定后續單元狀態的方式并非將當前狀態與新輸入相乘,而是將兩者相加,這正是LSTM的特別之處。(當然,遺忘門依舊使用乘法。)
不同的權重集對輸入信息進行篩選,決定是否輸入、輸出或遺忘。遺忘門的形式是一個線性恒等函數,因為如果門打開,則記憶單元的當前狀態就只會與1相乘,正向傳播一個時間步。
此外,講到簡單的竅門,將每個LSTM單元遺忘門的偏差設定為1,經證明可以提升網絡表現。(但Sutskever建議將偏差設定5。)
你可能會問,如果LSTM的目的是將遠距離事件與最終的輸出聯系起來,那為什么需要有遺忘門?因為有時候遺忘是件好事。以分析一個文本語料庫為例,在到達文檔的末尾時,你可能會認為下一個文檔與這個文檔肯定沒有任何聯系,所以記憶單元在開始吸收下一個文檔的第一項元素前應當先歸零。
在下圖中可以看到門的運作方式,其中橫線代表關閉的門,而空心小圓圈則代表打開的門。在隱藏層下方水平一行的橫線和圓圈就是遺忘門。
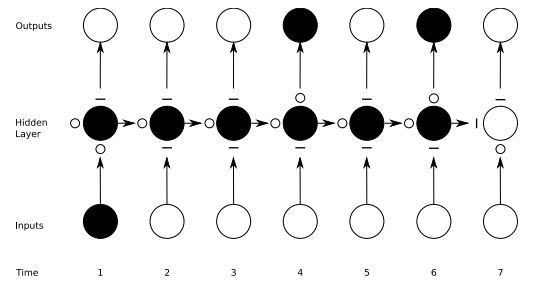
應當注意的是,前饋網絡只能將一個輸入映射至一個輸出,而遞歸網絡則可以像上圖那樣將一個輸入映射至多個輸出(從一張圖像到標題中的許多詞),也可以進行多對多(翻譯)或多對一(語音分類)的映射。
涵蓋多種時間尺度和遠距離依賴
你可能還會問,輸入門阻止新數據進入記憶單元,輸出門阻止記憶單元影響RNN特定輸出,此時這兩種門確切的值如何呢?可以認為LSTM相當于允許一個神經網絡同時在不同時間尺度上運行。
以一個人的人生為例,想象一下我們如何以一個時間序列的形式接收有關的這一人生不同數據流。就地理位置而言,每個時間步的位置對下一個時間步都相當重要, 所以地理位置的時間尺度就是始終對的信息保持開放。
假設這個人是位模范公民,每隔幾年就會投票。就民主生活的時間尺度而言,我們希望特別注意這個人在選舉前后所做的事,關注這個人在擱下重大議題、回歸日常生活之前的所作所為。我們不希望我們的政治分析被持續更新的地理位置信息所干擾。
如果這人還是個模范女兒,那我們或許可以增加家庭生活的時間尺度,了解到她打電話的模式是每周日一次,而每年過節期間電話量會大幅增加。這與政治活動周期和地理位置無關。
其他數據也是如此。音樂有復合節拍。文本包含按不同間隔反復出現的主題。股票市場和經濟體在長期波動之余還會經歷短期震蕩。這些事件同時在不同的時間尺度上進行,而LSTM可以涵蓋所有這些時間尺度。
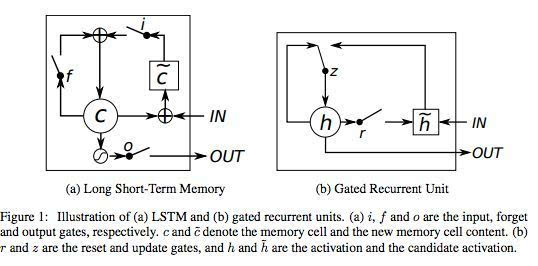
門控遞歸單元(GRU)
門控遞歸單元(GRU)本質上就是一個沒有輸出門的LSTM,因此它在每個時間步都會將記憶單元中的所有內容寫入整體網絡。
LSTM超參數調試
以下是手動優化RNN超參數時需要注意的一些事:
小心出現過擬合,這通常是因為神經網絡在“死記”定型數據。過擬合意味著定型數據的表現會很好,但網絡的模型對于樣例以外的預測則完全無用。
正則化有好處:正則化的方法包括l1、l2和丟棄法等。
保留一個神經網絡不作定型的多帶帶測試集。
網絡越大,功能越強,但也更容易過擬合。不要嘗試用10,000個樣例來學習一百萬個參數參數 > 樣例數 = 問題。
數據基本上總是越多越好,因為有助于防止過擬合。
定型應當包括多個epoch(使用整個數據集定型一次)。
每個epoch之后,評估測試集表現,判斷何時停止(提前停止)。
學習速率是更為重要的超參數。可用deeplearning4j-ui調試;
總體而言,堆疊層是有好處的。
對于LSTM,可使用softsign(而非softmax)激活函數替代tanh(更快且更不容易出現飽和(約0梯度))。
更新器:RMSProp、AdaGrad或momentum(Nesterovs)通常都是較好的選擇。AdaGrad還能衰減學習速率,有時會有幫助。
最后,記住數據標準化、MSE損失函數 + 恒等激活函數用于回歸、Xavier權重初始化
注
1) 雖然遞歸網絡可能距離通用人工智能還很遙遠,但我們相信,智能實際上比我們所想的要“笨”。也就是說,有了簡單的反饋循環作為記憶,我們就有了意識的基本元素之一-一項必要但不充分條件。上文沒有提到的其他條件可能包括表示網絡及其狀態的額外變量,以及基于數據解釋的決策邏輯框架。理想狀態下,后者會成為一個更大的問題解決循環的一部分,獎勵成功,懲罰失敗,與強化學習十分相似。話說,DeepMind已經造出了這樣的框架……
2) 所有參數經過優化的神經網絡在某種意義上都具有記憶,因為這些參數是過往數據的痕跡。但在前饋網絡中,這種記憶可能被凍結在了過去。也就是說,當網絡定型后,它所學習的模型可能被應用于更多數據,而不再對自身進行調整。此外,這類網絡也具有單體性,即將同樣的記憶(或權重集)應用于所有輸入數據。遞歸網絡有時也稱為動態(意為:“不斷變化的”)神經網絡,它與前饋網絡的較大區別不在于擁有記憶,而是它能夠將特定權重賦予以序列方式發生的多個事件。雖然這些事件不一定需要緊密相連,但網絡會假定它們都被同一根時間線聯系起來,不論距離多遠。前饋網絡則不會進行這樣的假設。它們將世界視為不具備時間次序的一堆對象。將這兩種神經網絡與兩種人類知識做類比可能會有助于理解。小時候,我們學習辨認顏色,然后我們這一輩子不論在何處都能認出各種顏色,在差別極大的各類情景中都是如此,也不受時間影響。顏色我們只需要學習一次。這種知識就像是前饋網絡的記憶:它們依賴于一種沒有范圍、無限定的過往信息。它們不知道也不關心五分鐘之前輸入的是什么顏色。前饋網絡有短期失憶癥。而另一方面,我們小時候還會學習如何解讀名為語言的聲音信號流,我們從這些聲音中提取出的意義,比如“toe”、“roe”或“z”,始終高度依賴于在其前后出現的聲音信號。序列的每一步都建立在前一步的基礎上,而意義產生于它們的順序。的確,句子中每個音節的意義是由許多個整句所共同傳達的,而句子中的冗余信號則是抵抗環境噪聲的保護。遞歸網絡的記憶與此類似,它們依賴的是過往信息中的一個特定片段。兩種網絡以不同的方式讓不同的過往信息發揮作用。
歡迎加入本站公開興趣群商業智能與數據分析群
興趣范圍包括各種讓數據產生價值的辦法,實際應用案例分享與討論,分析工具,ETL工具,數據倉庫,數據挖掘工具,報表系統等全方位知識
QQ群:81035754
文章版權歸作者所有,未經允許請勿轉載,若此文章存在違規行為,您可以聯系管理員刪除。
轉載請注明本文地址:http://m.specialneedsforspecialkids.com/yun/4391.html
摘要:設計用于處理序列依賴性的強大類型的神經網絡稱為復現神經網絡。你會知道關于國際航空公司乘客時間序列預測問題。感謝所有指出這個問題的人和菲利普奧布萊恩幫助提出的解決方案。 段哥http://machinelearningmastery... Time Series Prediction with LSTM Recurrent Neural Networks in Python with K...
摘要:得到的結果如下上圖是門卷積神經網絡模型與和模型在數據集基準上進行測試的結果。雖然在這一研究中卷積神經網絡在性能上表現出了對遞歸神經網絡,尤其是的全面超越,但是,現在談取代還為時尚早。 語言模型對于語音識別系統來說,是一個關鍵的組成部分,在機器翻譯中也是如此。近年來,神經網絡模型被認為在性能上要優于經典的 n-gram 語言模型。經典的語言模型會面臨數據稀疏的難題,使得模型很難表征大型的文本,...
摘要:因為在每一時刻對過去的記憶信息和當前的輸入處理策略都是一致的,這在其他領域如自然語言處理,語音識別等問題不大,但并不適用于個性化推薦,一個用戶的聽歌點擊序列,有正負向之分。 在內容爆炸性增長的今天,個性化推薦發揮著越來越重要的作用,如何在海量的數據中幫助用戶找到感興趣的物品,成為大數據領域極具挑戰性的一項工作;另一方面,深度學習已經被證明在圖像處理,計算機視覺,自然語言處理等領域都取得了不俗...
摘要:作為解決方案的和和是解決短時記憶問題的解決方案,它們具有稱為門的內部機制,可以調節信息流。隨后,它可以沿著長鏈序列傳遞相關信息以進行預測,幾乎所有基于遞歸神經網絡的技術成果都是通過這兩個網絡實現的。和采用門結構來克服短時記憶的影響。 短時記憶RNN 會受到短時記憶的影響。如果一條序列足夠長,那它們將很難將信息從較早的時間步傳送到后面的時間步。 因此,如果你正在嘗試處理一段文本進行預測,RNN...
閱讀 3273·2021-09-22 16:06
閱讀 3260·2021-09-02 15:40
閱讀 642·2019-08-30 15:54
閱讀 1047·2019-08-26 12:22
閱讀 1391·2019-08-26 12:17
閱讀 2753·2019-08-26 12:09
閱讀 513·2019-08-26 10:20
閱讀 796·2019-08-23 16:28