摘要：成本函數成本對于線性回歸，成本函數是表示每個預測值與其預期結果之間的聚合差異的某些函數對于邏輯回歸，是計算每次預測的正確或錯誤的某些函數。成本函數的變換涉及到預測結果和實際結果之間數值距離的任何函數都不能作為成本函數。

矩陣和多特征線性回歸

快速回顧

之前文章的前提是：給定特征——任何房屋面積（sqm），我們需要預測結果，也就是對應房價（$）。為了做到這一點，我們：

我們找到一條「最擬合」所有數據點的直線（線性回歸）。「最擬合」是當線性回歸線確保實際數據點（灰色點）和預測值（內插在直線上的灰色點）之間的差異最小，即最小化多個藍線之和。

使用這條直線，我們可以預測任何房屋的價格。

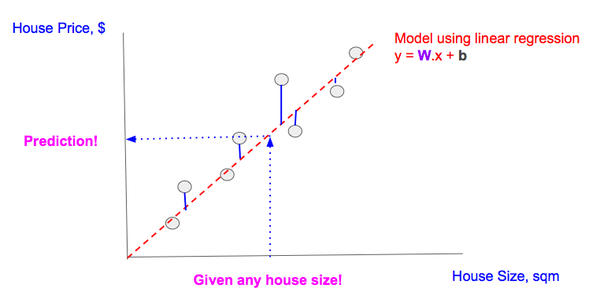
使用單一特征線性回歸進行預測

多特征線性回歸概述

實際上，任何預測都依賴于多個特征，于是我們從單特征的線性回歸進階到 帶有兩個特征的線性回歸；之所以選擇兩個特征，是為了讓可視化和理解簡明些，但這個思想可以推廣到帶有任何數量特征的線性回歸。

我們引進一個新的特征——房間數量。當收集數據點時，現在我們需要在現有特征「房屋面積」之上收集新特征「房間數」的值，以及相應的結果「房屋價格」。

我們的圖表變成了 3 維的。

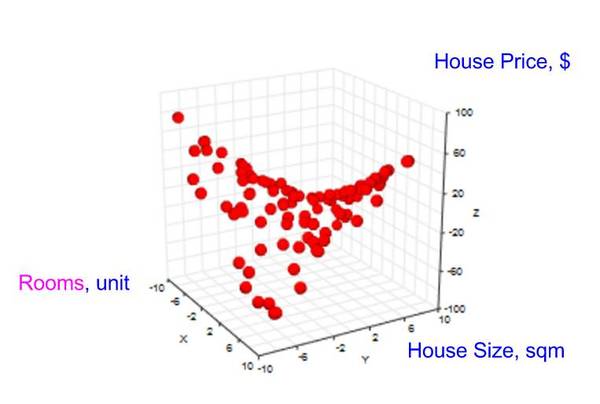
結果「房屋價格」以及 2 個特征（「房間數」，「房屋面積」）的數據點空間

然后，我們的目標變成：給定「房間數」和「房屋面積」，預測「房屋價格」（見下圖）。

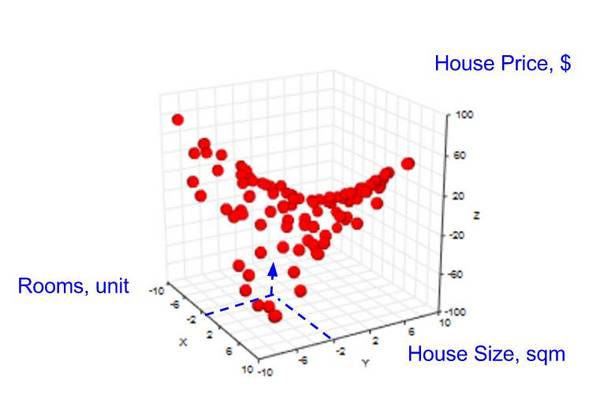
由于缺少數據點，有時無法對給定的 2 個特征進行預測

在單一特征的情形中，當沒有數據點時，我們需要使用線性回歸來創建一條直線，以幫助我們預測結果房屋價格。在 2 個特征的情形中，我們也可以使用線性回歸，但是需要創建一個平面（而不是直線），以幫助我們預測（見下圖）。

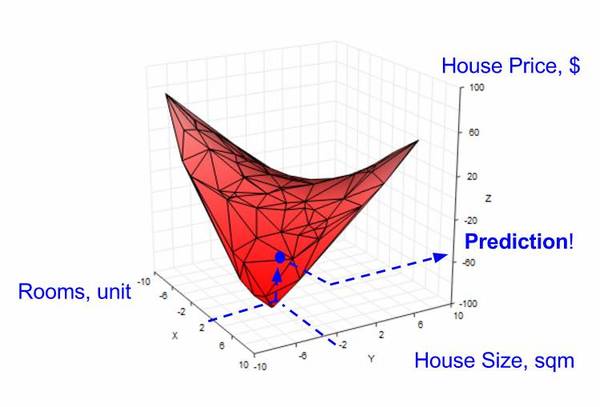
使用線性回歸在 2 個特征空間中的創建一個平面來做預測

多特征線性回歸模型

回憶單一特征的線性回歸（見下圖左邊），線性回歸模型結果為 y，權重為 W，房屋大面積為 x，偏差為 b。

對于 2 個特征的回歸（參見下圖右側），我們引入另一個權重 W2，另一個自變量 x2 來代表房間數的特征值。

單特征 vs. 2 個特征的線性回歸方程

如之前討論的那樣，當我們執行線性回歸時，梯度下降算法能幫助學習系數 W、W2 和 b 的值。

Tensorflow 的多特征線性回歸

1.快速回顧

單特征線性回歸的 TF 代碼由 3 部分組成（見下圖）：

構建模型（藍色部分）

基于模型構建成本函數（紅色部分）

使用梯度下降（綠色部分）最小化成本函數

用于單特征線性回歸的 Tensorflow 代碼

2.Tensorflow 的 2 個特征的線性回歸

TF 代碼中 2 個特征的線性回歸方程（如上所述）的變化（相比單特征）用紅色顯示。

注意，增加新特征的這種方式效率低；隨著特征數量的增長，所需的變量系數和自變量的數量會增加。實際的模型有更多的特征，這惡化了這個問題。那么，如何能有效地表示特征呢？

解決方法：矩陣

首先，讓我們將表征兩個特征的模型推廣到表征 n 個特征的模型：

復雜的 n 特征公式可以用矩陣簡化，矩陣被內置于 TF 中，這是因為：

數據可以用多維表示，這契合我們表征具有 n 個特征的數據點（左下方，也稱為特征矩陣）以及具有 n 個權重模型（右下，也稱為權重矩陣）的方式

單個數據點的 n 個特征與模型的矩陣形式的 n 個權重

在 TF 中，它們將被寫為：

x = tf.placeholder（tf.float，[1，n]）

W = tf.Variable（tf.zeros [n，1]）

注意：對于 W，我們使用 tf.zeros，它將所有 W1，W2，...，Wn 初始化為零。

在數學上，矩陣乘法是向量乘法的加總；因此自然地，特征（中間的一個）和權重（右邊的）矩陣之間的矩陣乘法給出（左邊的）結果，即等于 n 個特征的線性回歸公式的第一部分（如上所述），沒有截距項。

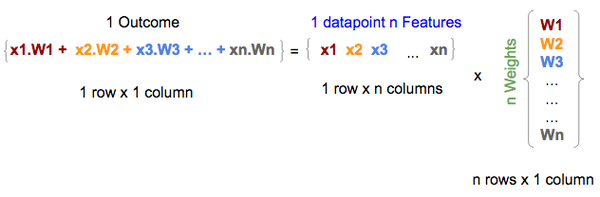
特征和權重矩陣之間的矩陣乘法給出結果（未添加截距項）

在 TF 中，這種乘法將表示為：

y = tf.matmul(x, W)

多行特征矩陣（每行表示數據點的 n 個特征）之間的矩陣乘法返回多行結果，每行代表每個數據點的結果/預測（沒有加入截距項）；因此一個矩陣乘法就可以將線性回歸公式應用于多個數據點，并對應地產生多個預測（每個數據點對應一個結果）（見下文）

注意：特征矩陣中的 x 表示變的更復雜，即我們使用 x1.1、x1.2，而不是 x1、x2 等，因為特征矩陣（中間矩陣）從表示 n 個特征（1 行 x，n 列）的單個數據點擴展到表示具有 n 個特征（m 行 x，n 列）的 m 個數據點。因此，我們擴展 x （如 x1）到 x .（如 x1.1），其中，n 是特征數，m 是數據點的數量。

具有模型權重的多行矩陣乘法產生矩陣的多個行結果

在 TF 中，它們將被寫為：

x = tf.placeholder（tf.float，[m，n]）

W = tf.Variable（tf.zeros [n，1]）

y = tf.matmul（x，W）

最后，向結果矩陣添加常數，也就是將常數添加到矩陣中的每一行

在 TF 中，用矩陣表示 x 和 W，無論模型的特征數量或要處理的數據點數量，矩陣都可以簡化為：

b = tf.Variable(tf.zeros[1])

y = tf.matmul(x, W) + b

Tensorflow 的多特征備忘單

我們做一個從單一特征到多特征的線性回歸的變化的并行比較：

Tensorflow 中的單特征與 n 個特征的線性回歸模型

總結

在本文中，我們介紹了多特征線性回歸的概念，并展示了我們如何將模型和 TF 代碼從單特征的線性回歸模型擴展到 2 個特征的線性回歸模型，并可以推廣到 n 特征線性回歸模型。最后我們為多特征的 TF 線性回歸模型提供了一張備忘單。

邏輯回歸

邏輯回歸綜述

我們已經學會了如何使用 Tensorflow（TF）去實現線性回歸以預測標量值得結果，例如給定一組特征，如住房大小，預測房價。

然而，有時我們需要對事物分類（classify）而不是去預測一個具體的數值，例如給定一張含有數字（0-9 十個數字中的一個）的圖片，我們需要將其分類為 0，1，2，3，4，5，6，7，8，9 十類。或者，我們需要將一首歌曲進行歸類，如歸類為流行，搖滾，說唱等。集合 [0,1,2，...，9]、[流行，搖滾，說唱，等等] 中的每一個元素都可以表示一個類。在計算機中，我們通常用數字對抽象名詞進行表示，比如，pop = 0, rock = 1, 等等。為了實現分類，我們使用 TF 來實現邏輯回歸。

在本文中，我們將使用邏輯回歸將數字圖片歸類為 0，1，2，3，4，5，6，7，8，9 這十類。

邏輯回歸的細節

線性回歸中的許多概念仍然用于邏輯回歸之中。我們可以再次使用公式 y = W.x + b，但是有一些不同的地方。讓我們看看線性回歸和邏輯回歸的公式：

線性回歸與邏輯回歸的區別與相似

區別：

結果（y）：對于線性回歸，結果是一個標量值（可以是任意一個符合實際的數值），例如 50000，23.98 等；對于邏輯回歸，結果是一個整數（表示不同類的整數，是離散的），例如 0,1,2，... 9。

特征（x）：對于線性回歸，特征都表示為一個列向量；對于涉及二維圖像的邏輯回歸，特征是一個二維矩陣，矩陣的每個元素表示圖像的像素值，每個像素值是屬于 0 到 255 之間的整數，其中 0 表示黑色，255 表示白色，其他值表示具有某些灰度陰影。

成本函數（成本）：對于線性回歸，成本函數是表示每個預測值與其預期結果之間的聚合差異的某些函數；對于邏輯回歸，是計算每次預測的正確或錯誤的某些函數。

相似性：

訓練：線性回歸和邏輯回歸的訓練目標都是去學習權重（W）和偏置（b）值。

結果：線性回歸與邏輯回歸的目標都是利用學習到的權重和偏置值去預測/分類結果。

協調邏輯回歸與線性回歸

為了使邏輯回歸利用 y = W.b + x，我們需要做出一些改變以協調上述差異。

1.特征變換，x

我們可以將二維的圖片特征（假設二維特征有 X 行，Y 列）轉換成一維的行向量：將第一行以外的其它行數值依順序放在第一行后面。

轉換圖像特征以適用于邏輯回歸公式

2.預測結果轉換，y

對于邏輯回歸，y 不能作為標量，因為預測可能最終為 2.3 或 11，這不在可能的類 [0,1，...，9] 中。

為了解決這個問題，y 應該被轉換成列向量，該向量的每個元素代表邏輯回歸模型認為屬于某個特定類的得分。在下面的示例中，預測結果為類"1"，因為它具有較高得分。

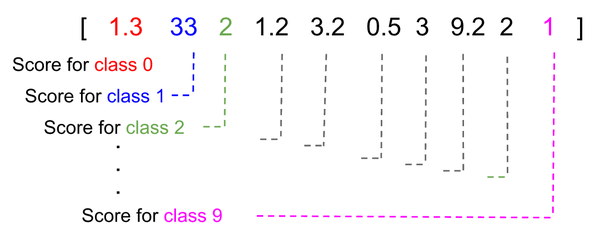
每個類的分數和具有較高分數的類成為被預測的類

對于給定的圖片，為求這個分數向量，每個像素都會貢獻一組分數（針對每一類），分數表示系統認為這張圖片屬于某類的可能性，每個像素分數之和成為預測向量。

每個像素提供一個分數向量；每個類別有一個分數，最后變成預測向量。所有預測向量的總和變成最終預測。

3.成本函數的變換

涉及到預測結果和實際結果之間數值距離的任何函數都不能作為成本函數。對于數字圖片「1」，這樣的成本函數將使預測值「7」（7-1=6）更嚴重地懲罰預測值「2」（2-1=1），盡管兩個預測結果都是錯誤的。

我們即將使用的成本函數，交叉熵（H），用以下幾個步驟實現：

1. 將實際圖片的類向量（y"）轉化成 one-hot 向量，這是一個概率分布。

2. 將預測類 (y) 轉化成概率分布。

3. 使用交叉熵函數去計算成本函數，這表示的是兩個概率分布函數之間的差異。

第一步：One-hot 向量

由于我們已經將預測 (y) 轉換成分數向量，因此，我們也應該將實際圖片類（y』）轉換成相同維數的向量；one-hot 向量是將對應于實際類的的元素為設為 1，其它元素為 0。下面，我們展示表示 0-9 十個類中一個類的 one-hot 向量。

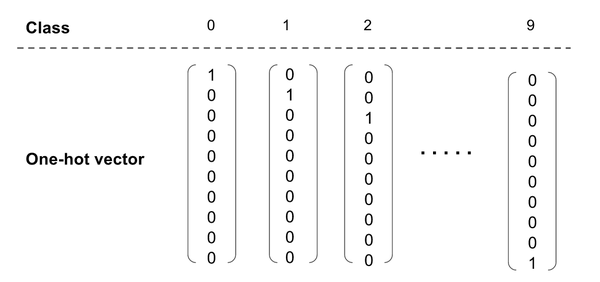
圖片類和它們的 one-hot 向量表示

假設實際圖像上是數字「1」(y")，它的 one-hot 向量是 [0,1,0,0,0,0,0,0,0,0]，假設其預測向量 (y) [1.3, 33, 2, 1.2, 3.2, 0.5, 3, 9.2, 1]，繪制比較如下：

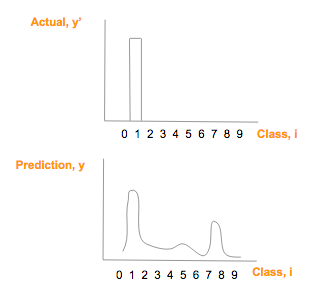
真實圖片 one—hot 向量（頂）預測類別概率

第二步：用 softmax 實現概率分布

為了在數學上比較這兩個「圖」的相似性，交叉熵是一個好方法。（這里是一個很棒但比較長的解釋，如果你對細節感興趣的話。https://colah.github.io/posts/2015-09-Visual-Information/）

然而，為了利用交叉熵，我們需要將實際結果向量（y"）和預測結果向量（y）轉換為「概率分布」，「概率分布」意味著：

每個類的概率/分數值在 0-1 之間；

所以類的概率/分數和必須是 1；

實際結果向量（y"）如果是 one-hot 向量，滿足了上述限制。

為預測結果向量（y）, 使用 softmax 將其轉換為概率分布：

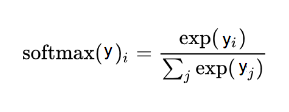
softmax 函數，這里 i 是表示 0, 1, 2, …, 9 十類

這個過程只需要簡單的兩步，預測向量（y）中的每個分量是 exp(y_i) 除以所有分量的 exp() 的和。

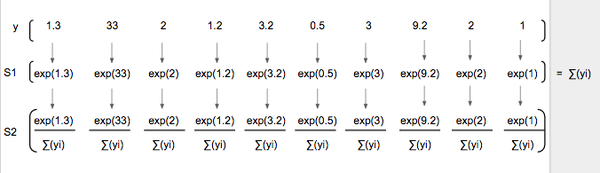
注意：softmax（y）圖形在形狀上與 prediction (y) 相似，但是僅僅有較大的較大值和較小的最小值

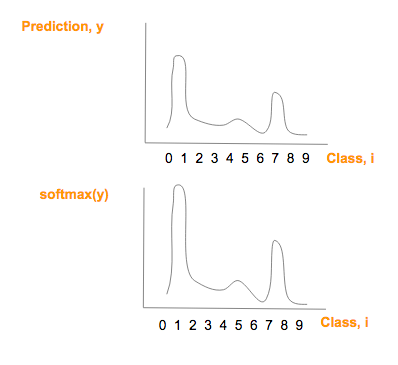
使用 softmax 前后預測（y）曲線

第三步：交叉熵

現在，我們將預測向量分數概率分布（y"）和實際向量分數概率分布 (y) 運用交叉熵。

交叉熵公式：

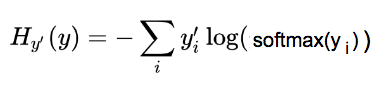
交叉熵作為我們想最小化的成本函數

為了快速理解這個復雜的公式，我們將其分為 3 部分（見下文）。注意，本文中的符號，我們使用 y_i 表示 y 的第 i 個分量。

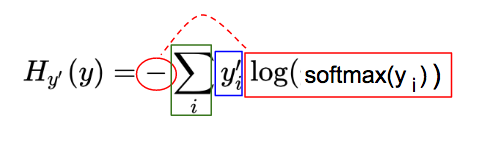
交叉熵（H）公式可視為三個部分：紅，藍，綠

藍：實際圖像類（y"）對應的 one-hot 圖，參看 one-hot 向量部分：

紅：由預測向量元素（y）經過softmax(y)，-og(softmax(y）一系列變化而來：

綠：每一圖片類別 i，其中，i = 0, 1, 2, …, 9, 紅藍部分相乘的結果

以下圖例會進一步簡化理解。

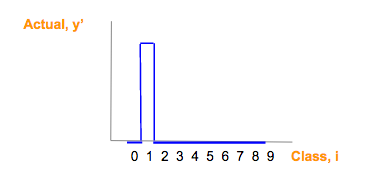
藍色制圖只是真實圖片類別（y"）one-hot 向量。

每個預測向量元素，y，轉換成 -log(softmax(y)，就得到紅圖：

預測類別向量（y）一系列轉換后，得到紅圖

如果你想完全地理解第二個變換 -log(softmax(y)) 與 softmax(y) 為什么成反比，請點擊 video or slides（參見文末資源部分）.

交叉熵（H），這個綠色的部分是每個類別的藍色值和紅色值的乘積和，然后將它們做如下相加：

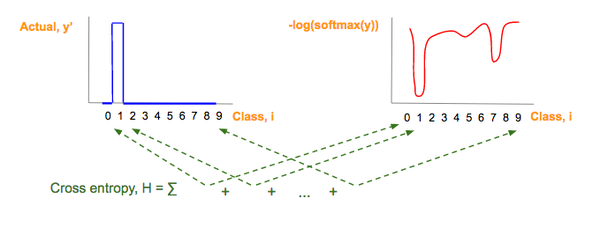
交叉熵是每個圖像類的藍色值和紅色值的乘積之和。

由于這張藍色圖片對應一個 one-hot 向量，one-hot 向量僅僅有一個元素是 1，它對應一個正確的圖片類，交叉熵的其它所有元素乘積為 0，交叉熵簡化為：

將所有部分放到一起

有了三個轉換后，現在，我們就可以將用于線性回歸的技術用于邏輯回歸。下面的代碼片段展示的是本系列文章第三部分線性回歸代碼和代碼適用邏輯回歸所需要的變化之間的對比。

邏輯回歸的目標是最小化交叉熵（H），這意味著我們只需要最小化 -log（softmax（y_i）項；因為該項與 softmax（y_i）成反比，所以我們實際上是較大化該項。

使用反向傳播去最小化交叉熵 (H ) 將改變邏輯回歸的權重 W 和偏置 b。因此，每張圖片的像素值將會給出對應圖片類較高分數/概率!（較高分數/概率對應于正確的圖片類）

將線性回歸方法用于邏輯回歸之中，「total_class」是欲分類問題的總類數量，例如，在上文手寫數字體識別例子中，total_class=10。

1. 將特征變換成一維特征；

2. 將預測結果向量、實際結果向量變化成 one-hot 向量；

3. 將成本函數從平方誤差函數變化到交叉熵。

總結

線性回歸對基于給定特征的預測（數值）是有幫助的，邏輯回歸根據輸入特征實現分類是有幫助的。

我們展示了如何調整線性回歸 y = W.x + b 實現邏輯回歸：（1）轉換特征向量；2）轉換預測/結果向量；（3）轉換成本函數。

當你掌握了 one-hot 向量，softmax，交叉熵的知識，你就可以處理谷歌上針對「初學者」的圖片分類問題。

資源：

針對初學者的圖像識別的谷歌代碼：https://github.com/tensorflow/tensorflow/blob/master/tensorflow/examples/tutorials/mnist/mnist_softmax.py

slideshare 上的幻燈片：http://www.slideshare.net/KhorSoonHin/gentlest-introduction-to-tensorflow-part-3

油管上的視頻：https://www.youtube.com/watch?v=F8g_6TXKlxw

原文鏈接：https://medium.com/all-of-us-are-belong-to-machines/gentlest-intro-to-tensorflow-4-logistic-regression-2afd0cabc54#.glculhxzi

商業智能與數據分析群

興趣范圍包括各種讓數據產生價值的辦法，實際應用案例分享與討論，分析工具，ETL工具，數據倉庫，數據挖掘工具，報表系統等全方位知識

QQ群：81035754