摘要：最普遍的變換是線性變換，即和均將規(guī)范化應(yīng)用于輸入的特征數(shù)據(jù)，而則另辟蹊徑，將規(guī)范化應(yīng)用于線性變換函數(shù)的權(quán)重，這就是名稱的來源。他們不處理權(quán)重向量，也不處理特征數(shù)據(jù)向量，就改了一下線性變換的函數(shù)其中是和的夾角。

“ 深度神經(jīng)網(wǎng)絡(luò)模型訓(xùn)練之難眾所周知，其中一個重要的現(xiàn)象就是 Internal Covariate Shift. Batch Normalization 大法自 2015 年由Google 提出之后，就成為深度學(xué)習(xí)必備之神器。自 BN 之后， Layer Norm / Weight Norm / Cosine Norm 等也橫空出世。本文從 Normalization 的背景講起，用一個公式概括 Normalization 的基本思想與通用框架，將各大主流方法一一對號入座進(jìn)行深入的對比分析，并從參數(shù)和數(shù)據(jù)的伸縮不變性的角度探討 Normalization 有效的深層原因。”

本文是該系列的第二篇。

03、主流 Normalization 方法梳理

在上一節(jié)中，我們提煉了 Normalization 的通用公式：

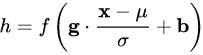
對照于這一公式，我們來梳理主流的四種規(guī)范化方法。

3.1 ?Batch Normalization —— 縱向規(guī)范化

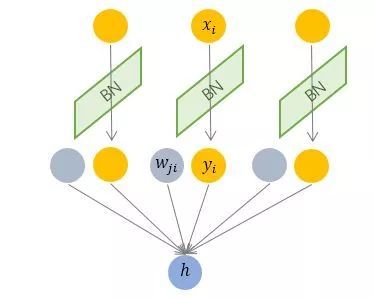
Batch Normalization 于2015年由 Google 提出，開 Normalization 之先河。其規(guī)范化針對單個神經(jīng)元進(jìn)行，利用網(wǎng)絡(luò)訓(xùn)練時一個 mini-batch 的數(shù)據(jù)來計算該神經(jīng)元 x_i 的均值和方差,因而稱為 Batch Normalization。

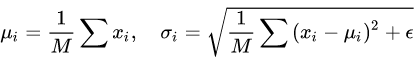
其中 M 是 mini-batch 的大小。

按上圖所示，相對于一層神經(jīng)元的水平排列，BN 可以看做一種縱向的規(guī)范化。由于 BN 是針對單個維度定義的，因此標(biāo)準(zhǔn)公式中的計算均為 element-wise 的。

BN 獨立地規(guī)范化每一個輸入維度 x_i ，但規(guī)范化的參數(shù)是一個 mini-batch 的一階統(tǒng)計量和二階統(tǒng)計量。這就要求 每一個 mini-batch 的統(tǒng)計量是整體統(tǒng)計量的近似估計，或者說每一個 mini-batch 彼此之間，以及和整體數(shù)據(jù)，都應(yīng)該是近似同分布的。分布差距較小的 mini-batch 可以看做是為規(guī)范化操作和模型訓(xùn)練引入了噪聲，可以增加模型的魯棒性；但如果每個 mini-batch的原始分布差別很大，那么不同 mini-batch 的數(shù)據(jù)將會進(jìn)行不一樣的數(shù)據(jù)變換，這就增加了模型訓(xùn)練的難度。

因此，BN 比較適用的場景是：每個 mini-batch 比較大，數(shù)據(jù)分布比較接近。在進(jìn)行訓(xùn)練之前，要做好充分的 shuffle. 否則效果會差很多。

另外，由于 BN 需要在運行過程中統(tǒng)計每個 mini-batch 的一階統(tǒng)計量和二階統(tǒng)計量，因此不適用于 動態(tài)的網(wǎng)絡(luò)結(jié)構(gòu) 和 RNN 網(wǎng)絡(luò)。不過，也有研究者專門提出了適用于 RNN 的 BN 使用方法，這里先不展開了。

3.2 Layer Normalization —— 橫向規(guī)范化

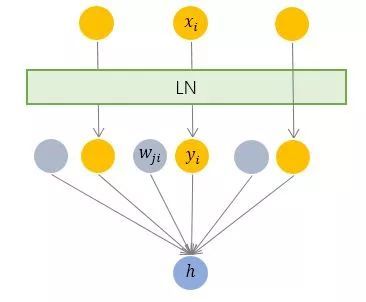
層規(guī)范化就是針對 BN 的上述不足而提出的。與 BN 不同，LN 是一種橫向的規(guī)范化，如圖所示。它綜合考慮一層所有維度的輸入，計算該層的平均輸入值和輸入方差，然后用同一個規(guī)范化操作來轉(zhuǎn)換各個維度的輸入。

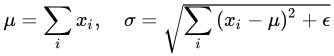
其中 i 枚舉了該層所有的輸入神經(jīng)元。對應(yīng)到標(biāo)準(zhǔn)公式中，四大參數(shù) μ, σ , b, g均為標(biāo)量（BN中是向量），所有輸入共享一個規(guī)范化變換。

LN 針對單個訓(xùn)練樣本進(jìn)行，不依賴于其他數(shù)據(jù)，因此可以避免 BN 中受 mini-batch 數(shù)據(jù)分布影響的問題，可以用于 小mini-batch場景、動態(tài)網(wǎng)絡(luò)場景和 RNN，特別是自然語言處理領(lǐng)域。此外，LN 不需要保存 mini-batch 的均值和方差，節(jié)省了額外的存儲空間。

但是，BN 的轉(zhuǎn)換是針對單個神經(jīng)元可訓(xùn)練的——不同神經(jīng)元的輸入經(jīng)過再平移和再縮放后分布在不同的區(qū)間，而 LN 對于一整層的神經(jīng)元訓(xùn)練得到同一個轉(zhuǎn)換——所有的輸入都在同一個區(qū)間范圍內(nèi)。如果不同輸入特征不屬于相似的類別（比如顏色和大小），那么 LN 的處理可能會降低模型的表達(dá)能力。

3.3 Weight Normalization —— 參數(shù)規(guī)范化

前面我們講的模型框架

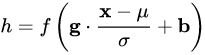
中，經(jīng)過規(guī)范化之后的 y 作為輸入送到下一個神經(jīng)元，應(yīng)用以 w 為參數(shù)的f_w() 函數(shù)定義的變換。最普遍的變換是線性變換，即?

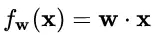
BN 和 LN 均將規(guī)范化應(yīng)用于輸入的特征數(shù)據(jù) x ，而 WN 則另辟蹊徑，將規(guī)范化應(yīng)用于線性變換函數(shù)的權(quán)重 w ，這就是 WN 名稱的來源。

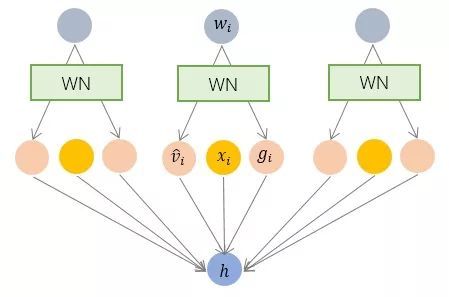
具體而言，WN 提出的方案是，將權(quán)重向量 w 分解為向量方向 v 和向量模 g 兩部分：

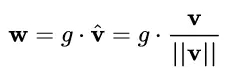
其中 v 是與 g 同維度的向量， ||v||是歐式范數(shù)，因此 v / ||v|| 是單位向量，決定了 w 的方向；g 是標(biāo)量，決定了 w 的長度。由于 ||w|| = |g| ，因此這一權(quán)重分解的方式將權(quán)重向量的歐氏范數(shù)進(jìn)行了固定，從而實現(xiàn)了正則化的效果。

乍一看，這一方法似乎脫離了我們前文所講的通用框架？

并沒有。其實從最終實現(xiàn)的效果來看，異曲同工。我們來推導(dǎo)一下看。?

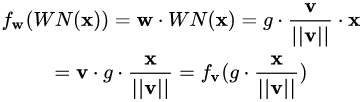
對照一下前述框架：

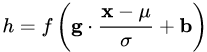
我們只需令：

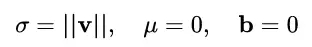
就完美地對號入座了！

回憶一下，BN 和 LN 是用輸入的特征數(shù)據(jù)的方差對輸入數(shù)據(jù)進(jìn)行 scale，而 WN 則是用 神經(jīng)元的權(quán)重的歐氏范式對輸入數(shù)據(jù)進(jìn)行 scale。雖然在原始方法中分別進(jìn)行的是特征數(shù)據(jù)規(guī)范化和參數(shù)的規(guī)范化，但本質(zhì)上都實現(xiàn)了對數(shù)據(jù)的規(guī)范化，只是用于 scale 的參數(shù)來源不同。

另外，我們看到這里的規(guī)范化只是對數(shù)據(jù)進(jìn)行了 scale，而沒有進(jìn)行 shift，因為我們簡單地令 μ = 0. 但事實上，這里留下了與 BN 或者 LN 相結(jié)合的余地——那就是利用 BN 或者 LN 的方法來計算輸入數(shù)據(jù)的均值 μ。

WN 的規(guī)范化不直接使用輸入數(shù)據(jù)的統(tǒng)計量，因此避免了 BN 過于依賴 mini-batch 的不足，以及 LN 每層轉(zhuǎn)換器的限制，同時也可以用于動態(tài)網(wǎng)絡(luò)結(jié)構(gòu)。

3.4 Cosine Normalization —— 余弦規(guī)范化

Normalization 還能怎么做？

我們再來看看神經(jīng)元的經(jīng)典變換?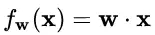

對輸入數(shù)據(jù) x 的變換已經(jīng)做過了，橫著來是 LN，縱著來是 BN。

對模型參數(shù) w 的變換也已經(jīng)做過了，就是 WN。

好像沒啥可做的了。

然而天才的研究員們盯上了中間的那個點，對，就是 ·

他們說，我們要對數(shù)據(jù)進(jìn)行規(guī)范化的原因，是數(shù)據(jù)經(jīng)過神經(jīng)網(wǎng)絡(luò)的計算之后可能會變得很大，導(dǎo)致數(shù)據(jù)分布的方差爆炸，而這一問題的根源就是我們的計算方式——點積，權(quán)重向量 w 和 特征數(shù)據(jù)向量 x 的點積。向量點積是無界（unbounded）的啊！

那怎么辦呢？我們知道向量點積是衡量兩個向量相似度的方法之一。哪還有沒有其他的相似度衡量方法呢？有啊，很多啊！夾角余弦就是其中之一啊！而且關(guān)鍵的是，夾角余弦是有確定界的啊，[-1, 1] 的取值范圍，多么的美好！仿佛看到了新的世界！

于是，Cosine Normalization 就出世了。他們不處理權(quán)重向量 w ，也不處理特征數(shù)據(jù)向量 x ，就改了一下線性變換的函數(shù)：

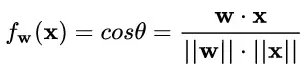
其中 θ 是 w 和 x 的夾角。然后就沒有然后了，所有的數(shù)據(jù)就都是 [-1, 1] 區(qū)間范圍之內(nèi)的了！

不過，回過頭來看，CN 與 WN 還是很相似的。我們看到上式中，分子還是 w 和 x 的內(nèi)積，而分母則可以看做用 w 和 x 二者的模之積進(jìn)行規(guī)范化。對比一下 WN 的公式：

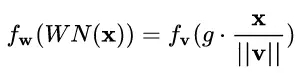
一定程度上可以理解為，WN 用 權(quán)重的模 ||v|| 對輸入向量進(jìn)行 scale，而 CN 在此基礎(chǔ)上用輸入向量的模 ||x|| 對輸入向量進(jìn)行了進(jìn)一步的 scale.

CN 通過用余弦計算代替內(nèi)積計算實現(xiàn)了規(guī)范化，但成也蕭何敗蕭何。原始的內(nèi)積計算，其幾何意義是 輸入向量在權(quán)重向量上的投影，既包含 二者的夾角信息，也包含 兩個向量的scale信息。去掉scale信息，可能導(dǎo)致表達(dá)能力的下降，因此也引起了一些爭議和討論。具體效果如何，可能需要在特定的場景下深入實驗。

現(xiàn)在，BN, LN, WN 和 CN 之間的來龍去脈是不是清楚多了？

04、Normalization 為什么會有效

我們以下面這個簡化的神經(jīng)網(wǎng)絡(luò)為例來分析。

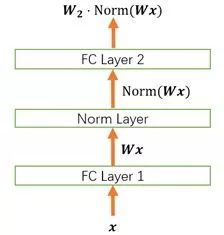
4.1 Normalization 的權(quán)重伸縮不變性

權(quán)重伸縮不變性（weight scale invariance）指的是，當(dāng)權(quán)重 W 按照常量 λ 進(jìn)行伸縮時，得到的規(guī)范化后的值保持不變，即：

其中 W" = λW 。

上述規(guī)范化方法均有這一性質(zhì)，這是因為，當(dāng)權(quán)重 ?W 伸縮時，對應(yīng)的均值和標(biāo)準(zhǔn)差均等比例伸縮，分子分母相抵。

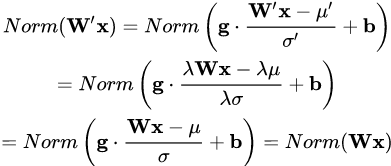
權(quán)重伸縮不變性可以有效地提高反向傳播的效率。由于

因此，權(quán)重的伸縮變化不會影響反向梯度的 Jacobian 矩陣，因此也就對反向傳播沒有影響，避免了反向傳播時因為權(quán)重過大或過小導(dǎo)致的梯度消失或梯度爆炸問題，從而加速了神經(jīng)網(wǎng)絡(luò)的訓(xùn)練。

權(quán)重伸縮不變性還具有參數(shù)正則化的效果，可以使用更高的學(xué)習(xí)率。由于

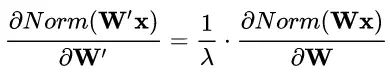
因此，下層的權(quán)重值越大，其梯度就越小。這樣，參數(shù)的變化就越穩(wěn)定，相當(dāng)于實現(xiàn)了參數(shù)正則化的效果，避免參數(shù)的大幅震蕩，提高網(wǎng)絡(luò)的泛化性能。進(jìn)而可以使用更高的學(xué)習(xí)率，提高學(xué)習(xí)速度。

4.2 Normalization 的數(shù)據(jù)伸縮不變性

數(shù)據(jù)伸縮不變性（data scale invariance）指的是，當(dāng)數(shù)據(jù) x 按照常量 λ 進(jìn)行伸縮時，得到的規(guī)范化后的值保持不變，即：

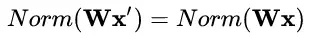
其中 x" = λx 。

數(shù)據(jù)伸縮不變性僅對 BN、LN 和 CN 成立。因為這三者對輸入數(shù)據(jù)進(jìn)行規(guī)范化，因此當(dāng)數(shù)據(jù)進(jìn)行常量伸縮時，其均值和方差都會相應(yīng)變化，分子分母互相抵消。而 WN 不具有這一性質(zhì)。

數(shù)據(jù)伸縮不變性可以有效地減少梯度彌散，簡化對學(xué)習(xí)率的選擇。

對于某一層神經(jīng)元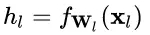而言，展開可得

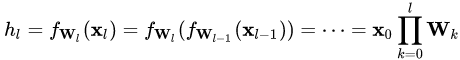
每一層神經(jīng)元的輸出依賴于底下各層的計算結(jié)果。如果沒有正則化，當(dāng)下層輸入發(fā)生伸縮變化時，經(jīng)過層層傳遞，可能會導(dǎo)致數(shù)據(jù)發(fā)生劇烈的膨脹或者彌散，從而也導(dǎo)致了反向計算時的梯度爆炸或梯度彌散。

加入 Normalization 之后，不論底層的數(shù)據(jù)如何變化，對于某一層神經(jīng)元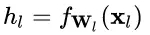?而言，其輸入 x_l 永遠(yuǎn)保持標(biāo)準(zhǔn)的分布，這就使得高層的訓(xùn)練更加簡單。從梯度的計算公式來看：

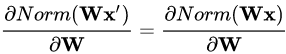
數(shù)據(jù)的伸縮變化也不會影響到對該層的權(quán)重參數(shù)更新，使得訓(xùn)練過程更加魯棒，簡化了對學(xué)習(xí)率的選擇。

[1] Sergey Ioffe and Christian Szegedy. Accelerating Deep Network Training by Reducing Internal Covariate Shift.（https://arxiv.org/abs/1502.03167 ）

[2] Jimmy L. Ba, Jamie R. Kiros, Geoffrey E. Hinton. [1607.06450] Layer Normalization.（https://arxiv.org/abs/1607.06450 ）

[3] Tim Salimans, Diederik P. Kingma. A Simple Reparameterization to Accelerate Training of Deep Neural Networks.（https://arxiv.org/abs/1602.07868 ）

[4] Chunjie Luo, Jianfeng Zhan, Lei Wang, Qiang Yang. Using Cosine Similarity Instead of Dot Product in Neural Networks.（https://arxiv.org/abs/1702.05870 ）

[5] Ian Goodfellow, Yoshua Bengio, Aaron Courville. Deep Learning.（http://www.deeplearningbook.org/ ）歡迎加入本站公開興趣群

商業(yè)智能與數(shù)據(jù)分析群

興趣范圍包括各種讓數(shù)據(jù)產(chǎn)生價值的辦法，實際應(yīng)用案例分享與討論，分析工具，ETL工具，數(shù)據(jù)倉庫，數(shù)據(jù)挖掘工具，報表系統(tǒng)等全方位知識

QQ群：81035754