摘要：事實上，我記得確實有一些教程是直接通過微分方程來定義函數的。歐拉的解法來源很簡單，就是用來近似導數項。這樣一來，我們就知道的歐拉解法實際上就是的一個特例罷了。

作者丨蘇劍林

單位丨廣州火焰信息科技有限公司

研究方向丨NLP，神經網絡

個人主頁丨kexue.fm

本來筆者已經決心不玩 RNN 了，但是在上個星期思考時忽然意識到 RNN 實際上對應了 ODE（常微分方程）的數值解法，這為我一直以來想做的事情——用深度學習來解決一些純數學問題——提供了思路。事實上這是一個頗為有趣和有用的結果，遂介紹一翻。順便地，本文也涉及到了自己動手編寫 RNN 的內容，所以本文也可以作為編寫自定義的 RNN 層的一個簡單教程。

注：本文并非前段時間的熱點“神經 ODE [1]”的介紹（但有一定的聯系）。

RNN基本

什么是RNN？?

眾所周知，RNN 是“循環神經網絡（Recurrent Neural Network）”，跟 CNN 不同，RNN 可以說是一類模型的總稱，而并非單個模型。簡單來講，只要是輸入向量序列 (x1,x2,…,xT)，輸出另外一個向量序列 (y1,y2,…,yT)，并且滿足如下遞歸關系的模型，都可以稱為 RNN。

也正因為如此，原始的樸素 RNN，還有改進的如 GRU、LSTM、SRU 等模型，我們都稱為 RNN，因為它們都可以作為上式的一個特例。還有一些看上去與 RNN 沒關的內容，比如前不久介紹的 CRF 的分母的計算，實際上也是一個簡單的 RNN。

說白了，RNN 其實就是遞歸計算。

自己編寫RNN

這里我們先介紹如何用 Keras 簡單快捷地編寫自定義的 RNN。?

事實上，不管在 Keras 還是純 tensorflow 中，要自定義自己的 RNN 都不算復雜。在 Keras 中，只要寫出每一步的遞歸函數；而在 tensorflow 中，則稍微復雜一點，需要將每一步的遞歸函數封裝為一個 RNNCell 類。

下面介紹用 Keras 實現最基本的一個 RNN：

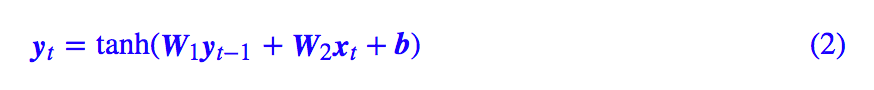
代碼非常簡單：

#! -*- coding: utf-8- -*-

from keras.layers import Layer

import keras.backend as K

class My_RNN(Layer):

? ? def __init__(self, output_dim, **kwargs):

? ? ? ? self.output_dim = output_dim # 輸出維度

? ? ? ? super(My_RNN, self).__init__(**kwargs)

? ? def build(self, input_shape): # 定義可訓練參數

? ? ? ? self.kernel1 = self.add_weight(name="kernel1",

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? shape=(self.output_dim, self.output_dim),

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? initializer="glorot_normal",

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? trainable=True)

? ? ? ? self.kernel2 = self.add_weight(name="kernel2",

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? shape=(input_shape[-1], self.output_dim),

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? initializer="glorot_normal",

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? trainable=True)

? ? ? ? self.bias = self.add_weight(name="kernel",

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? shape=(self.output_dim,),

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? initializer="glorot_normal",

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? trainable=True)

? ? def step_do(self, step_in, states): # 定義每一步的迭代

? ? ? ? step_out = K.tanh(K.dot(states[0], self.kernel1) +

? ? ? ? ? ? ? ? ? ? ? ? ? K.dot(step_in, self.kernel2) +

? ? ? ? ? ? ? ? ? ? ? ? ? self.bias)

? ? ? ? return step_out, [step_out]

? ? def call(self, inputs): # 定義正式執行的函數

? ? ? ? init_states = [K.zeros((K.shape(inputs)[0],

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? self.output_dim)

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? )] # 定義初始態(全零)

? ? ? ? outputs = K.rnn(self.step_do, inputs, init_states) # 循環執行step_do函數

? ? ? ? return outputs[0] # outputs是一個tuple，outputs[0]為最后時刻的輸出，

? ? ? ? ? ? ? ? ? ? ? ? ? # outputs[1]為整個輸出的時間序列，output[2]是一個list，

? ? ? ? ? ? ? ? ? ? ? ? ? # 是中間的隱藏狀態。

? ? def compute_output_shape(self, input_shape):

? ? ? ? return (input_shape[0], self.output_dim)

可以看到，雖然代碼行數不少，但大部分都只是固定格式的語句，真正定義 RNN 的，是 step_do 這個函數，這個函數接受兩個輸入：step_in 和 states。其中 step_in 是一個 (batch_size, input_dim) 的張量，代表當前時刻的樣本 xt，而 states 是一個 list，代表 yt?1 及一些中間變量。

特別要注意的是，states 是一個張量的 list，而不是單個張量，這是因為在遞歸過程中可能要同時傳遞多個中間變量，而不僅僅是 yt?1 一個，比如 LSTM 就需要有兩個態張量。最后 step_do 要返回 yt 和新的 states，這是 step_do 這步的函數的編寫規范。?

而 K.rnn 這個函數，接受三個基本參數（還有其他參數，請自行看官方文檔），其中第一個參數就是剛才寫好的 step_do 函數，第二個參數則是輸入的時間序列，第三個是初始態，跟前面說的 states 一致，所以很自然 init_states 也是一個張量的 list，默認情況下我們會選擇全零初始化。

ODE基本

什么是ODE？

ODE 就是“常微分方程（Ordinary Differential Equation）”，這里指的是一般的常微分方程組：

研究 ODE 的領域通常也直接稱為“動力學”、“動力系統”，這是因為牛頓力學通常也就只是一組 ODE 而已。

ODE可以產生非常豐富的函數。比如 e^t 其實就是 x˙=x 的解，sint 和 cost 都是 x¨+x=0 的解（初始條件不同）。事實上，我記得確實有一些教程是直接通過微分方程 x˙=x 來定義 e^t 函數的。除了這些初等函數，很多我們能叫得上名字但不知道是什么鬼的特殊函數，都是通過 ODE 導出來的，比如超幾何函數、勒讓德函數、貝塞爾函數...

總之，ODE 能產生并且已經產生了各種各樣千奇百怪的函數～

數值解ODE?

能較精確求出解析解的 ODE 其實是非常少的，所以很多時候我們都需要數值解法。?

ODE 的數值解已經是一門非常成熟的學科了，這里我們也不多做介紹，僅引入最基本的由數學家歐拉提出來的迭代公式：

這里的 h 是步長。歐拉的解法來源很簡單，就是用：

來近似導數項 x˙(t)。只要給定初始條件 x(0)，我們就可以根據 (4) 一步步迭代算出每個時間點的結果。

ODE與RNN?

ODE也是RNN

大家仔細對比 (4) 和 (1)，發現有什么聯系了嗎？

在 (1) 中，t 是一個整數變量，在 (4) 中，t 是一個浮點變量，除此之外，(4) 跟 (1) 貌似就沒有什么明顯的區別了。事實上，在 (4) 中我們可以以 h 為時間單位，記 t=nh，那么 (4) 變成了：

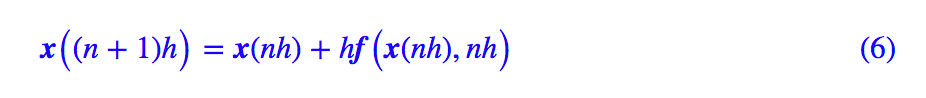
可以看到現在 (6) 中的時間變量 n 也是整數了。這樣一來，我們就知道：ODE 的歐拉解法 (4) 實際上就是 RNN 的一個特例罷了。這里我們也許可以間接明白為什么 RNN 的擬合能力如此之強了（尤其是對于時間序列數據），我們看到 ODE 可以產生很多復雜的函數，而 ODE 只不過是 RNN 的一個特例罷了，所以 RNN 也就可以產生更為復雜的函數了。?

用RNN解ODE?

于是，我們就可以寫一個 RNN 來解 ODE 了，比如《兩生物種群競爭模型》[2] 中的例子：

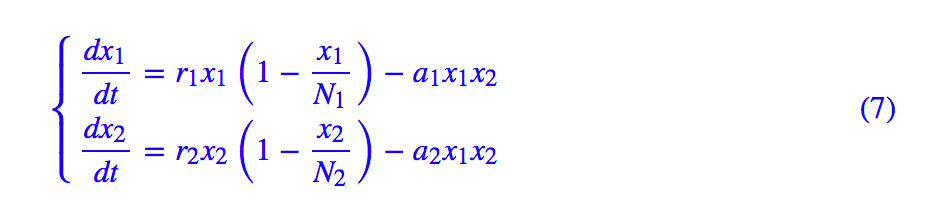
我們可以寫出：

#! -*- coding: utf-8- -*-

from keras.layers import Layer

import keras.backend as K

class ODE_RNN(Layer):

? ? def __init__(self, steps, h, **kwargs):

? ? ? ? self.steps = steps

? ? ? ? self.h = h

? ? ? ? super(ODE_RNN, self).__init__(**kwargs)

? ? def step_do(self, step_in, states): # 定義每一步的迭代

? ? ? ? x = states[0]

? ? ? ? r1,r2,a1,a2,iN1,iN2 = 0.1,0.3,0.0001,0.0002,0.002,0.003

? ? ? ? _1 = r1 * x[:,0] * (1 - iN1 * x[:,0]) - a1 * x[:,0] * x[:,1]

? ? ? ? _2 = r2 * x[:,1] * (1 - iN2 * x[:,1]) - a2 * x[:,0] * x[:,1]

? ? ? ? _1 = K.expand_dims(_1, 1)

? ? ? ? _2 = K.expand_dims(_2, 1)

? ? ? ? _ = K.concatenate([_1, _2], 1)

? ? ? ? step_out = x + self.h * _

? ? ? ? return step_out, [step_out]

? ? def call(self, inputs): # 這里的inputs就是初始條件

? ? ? ? init_states = [inputs]

? ? ? ? zeros = K.zeros((K.shape(inputs)[0],

? ? ? ? ? ? ? ? ? ? ? ? ?self.steps,

? ? ? ? ? ? ? ? ? ? ? ? ?K.shape(inputs)[1])) # 迭代過程用不著外部輸入，所以

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? # 指定一個全零輸入，只為形式上的傳入

? ? ? ? outputs = K.rnn(self.step_do, zeros, init_states) # 循環執行step_do函數

? ? ? ? return outputs[1] # 這次我們輸出整個結果序列

? ? def compute_output_shape(self, input_shape):

? ? ? ? return (input_shape[0], self.steps, input_shape[1])

from keras.models import Sequential

import numpy as np

import matplotlib.pyplot as plt

steps,h = 1000,0.1

M = Sequential()

M.add(ODE_RNN(steps, h, input_shape=(2,)))

M.summary()

# 直接前向傳播就輸出解了

result = M.predict(np.array([[100, 150]]))[0] # 以[100, 150]為初始條件進行演算

times = np.arange(1, steps+1) * h

# 繪圖

plt.plot(times, result[:,0])

plt.plot(times, result[:,1])

plt.savefig("test.png")

整個過程很容易理解，只不過有兩點需要指出一下。首先，由于方程組 (7) 只有兩維，而且不容易寫成矩陣運算，因此我在 step_do 函數中是直接逐位操作的（代碼中的 x[:,0],x[:,1]），如果方程本身維度較高，而且能寫成矩陣運算，那么直接利用矩陣運算寫會更加高效；然后，我們可以看到，寫完整個模型之后，直接 predict 就輸出結果了，不需要“訓練”。

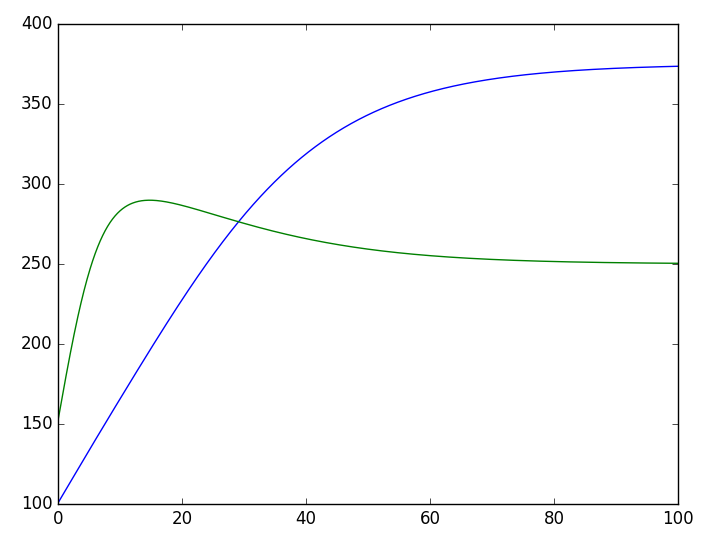
RNN解兩物種的競爭模型

反推ODE參數

前一節的介紹也就是說，RNN 的前向傳播跟 ODE 的歐拉解法是對應的，那么反向傳播又對應什么呢？

在實際問題中，有一類問題稱為“模型推斷”，它是在已知實驗數據的基礎上，猜測這批數據符合的模型（機理推斷）。這類問題的做法大概分兩步，第一步是猜測模型的形式，第二步是確定模型的參數。假定這批數據可以由一個 ODE 描述，并且這個 ODE 的形式已經知道了，那么就需要估計里邊的參數。

如果能夠用公式完全解出這個 ODE，那么這就只是一個非常簡單的回歸問題罷了。但前面已經說過，多數 ODE 都沒有公式解，所以數值方法就必須了。這其實就是 ODE 對應的 RNN 的反向傳播所要做的事情：前向傳播就是解 ODE（RNN 的預測過程），反向傳播自然就是推斷 ODE 的參數了（RNN 的訓練過程）。這是一個非常有趣的事實：ODE 的參數推斷是一個被研究得很充分的課題，然而在深度學習這里，只是 RNN 的一個最基本的應用罷了。

我們把剛才的例子的微分方程的解數據保存下來，然后只取幾個點，看看能不能反推原來的微分方程出來，解數據為：

假設就已知這有限的點數據，然后假定方程 (7) 的形式，求方程的各個參數。我們修改一下前面的代碼：

#! -*- coding: utf-8- -*-

from keras.layers import Layer

import keras.backend as K

def my_init(shape, dtype=None): # 需要定義好初始化，這相當于需要實驗估計參數的量級

? ? return K.variable([0.1, 0.1, 0.001, 0.001, 0.001, 0.001])

class ODE_RNN(Layer):

? ? def __init__(self, steps, h, **kwargs):

? ? ? ? self.steps = steps

? ? ? ? self.h = h

? ? ? ? super(ODE_RNN, self).__init__(**kwargs)

? ? def build(self, input_shape): # 將原來的參數設為可訓練的參數

? ? ? ? self.kernel = self.add_weight(name="kernel",?

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? shape=(6,),

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? initializer=my_init,

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? trainable=True)

? ? def step_do(self, step_in, states): # 定義每一步的迭代

? ? ? ? x = states[0]

? ? ? ? r1,r2,a1,a2,iN1,iN2 = (self.kernel[0], self.kernel[1],

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?self.kernel[2], self.kernel[3],

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?self.kernel[4], self.kernel[5])

? ? ? ? _1 = r1 * x[:,0] * (1 - iN1 * x[:,0]) - a1 * x[:,0] * x[:,1]

? ? ? ? _2 = r2 * x[:,1] * (1 - iN2 * x[:,1]) - a2 * x[:,0] * x[:,1]

? ? ? ? _1 = K.expand_dims(_1, 1)

? ? ? ? _2 = K.expand_dims(_2, 1)

? ? ? ? _ = K.concatenate([_1, _2], 1)

? ? ? ? step_out = x + self.h * K.clip(_, -1e5, 1e5) # 防止梯度爆炸

? ? ? ? return step_out, [step_out]

? ? def call(self, inputs): # 這里的inputs就是初始條件

? ? ? ? init_states = [inputs]

? ? ? ? zeros = K.zeros((K.shape(inputs)[0],

? ? ? ? ? ? ? ? ? ? ? ? ?self.steps,

? ? ? ? ? ? ? ? ? ? ? ? ?K.shape(inputs)[1])) # 迭代過程用不著外部輸入，所以

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? # 指定一個全零輸入，只為形式上的傳入

? ? ? ? outputs = K.rnn(self.step_do, zeros, init_states) # 循環執行step_do函數

? ? ? ? return outputs[1] # 這次我們輸出整個結果序列

? ? def compute_output_shape(self, input_shape):

? ? ? ? return (input_shape[0], self.steps, input_shape[1])

from keras.models import Sequential

from keras.optimizers import Adam

import numpy as np

import matplotlib.pyplot as plt

steps,h = 50, 1 # 用大步長，減少步數，削弱長時依賴，也加快推斷速度

series = {0: [100, 150],

? ? ? ? ? 10: [165, 283],

? ? ? ? ? 15: [197, 290],

? ? ? ? ? 30: [280, 276],

? ? ? ? ? 36: [305, 269],

? ? ? ? ? 40: [318, 266],

? ? ? ? ? 42: [324, 264]}

M = Sequential()

M.add(ODE_RNN(steps, h, input_shape=(2,)))

M.summary()

# 構建訓練樣本

# 其實就只有一個樣本序列，X為初始條件，Y為后續時間序列

X = np.array([series[0]])

Y = np.zeros((1, steps, 2))

for i,j in series.items():

? ? if i != 0:

? ? ? ? Y[0, int(i/h)-1] += series[i]

# 自定義loss

# 在訓練的時候，只考慮有數據的幾個時刻，沒有數據的時刻被忽略

def ode_loss(y_true, y_pred):

? ? T = K.sum(K.abs(y_true), 2, keepdims=True)

? ? T = K.cast(K.greater(T, 1e-3), "float32")

? ? return K.sum(T * K.square(y_true - y_pred), [1, 2])

M.compile(loss=ode_loss,

? ? ? ? ? optimizer=Adam(1e-4))

M.fit(X, Y, epochs=10000) # 用低學習率訓練足夠多輪

# 用訓練出來的模型重新預測，繪圖，比較結果

result = M.predict(np.array([[100, 150]]))[0]

times = np.arange(1, steps+1) * h

plt.clf()

plt.plot(times, result[:,0], color="blue")

plt.plot(times, result[:,1], color="green")

plt.plot(series.keys(), [i[0] for i in series.values()], "o", color="blue")

plt.plot(series.keys(), [i[1] for i in series.values()], "o", color="green")

plt.savefig("test.png")

結果可以用一張圖來看：

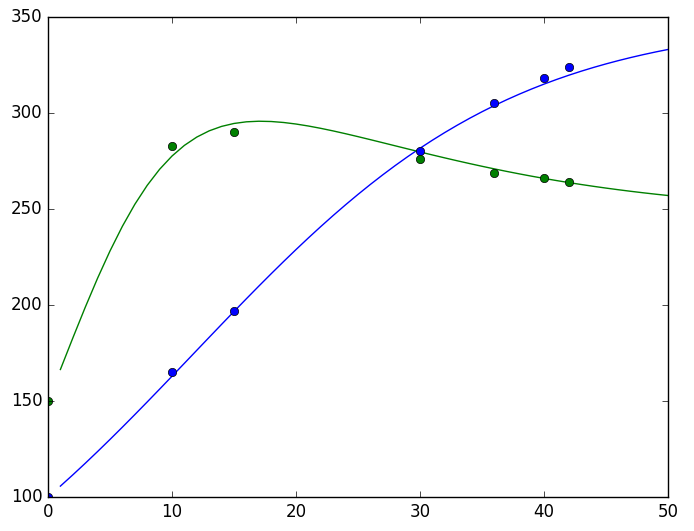
RNN做ODE的參數估計效果

（散點：有限的實驗數據，曲線：估計出來的模型）

顯然結果是讓人滿意的。

又到總結

本文在一個一般的框架下介紹了 RNN 模型及其在 Keras 下的自定義寫法，然后揭示了 ODE 與 RNN 的聯系。在此基礎上，介紹了用 RNN 直接求解 ODE 以及用 RNN 反推 ODE 參數的基本思路。

需要提醒讀者的是，在 RNN 模型的反向傳播中，要謹慎地做好初始化和截斷處理處理，并且選擇好學習率等，以防止梯度爆炸的出現（梯度消失只是優化得不夠好，梯度爆炸則是直接崩潰了，解決梯度爆炸問題尤為重要）。

總之，梯度消失和梯度爆炸在 RNN 中是一個很經典的困難，事實上，LSTM、GRU 等模型的引入，根本原因就是為了解決 RNN 的梯度消失問題，而梯度爆炸則是通過使用 tanh 或 sigmoid 激活函數來解決的。

但是如果用 RNN 解決 ODE 的話，我們就沒有選擇激活函數的權利了（激活函數就是 ODE 的一部分），所以只能謹慎地做好初始化及其他處理。據說，只要謹慎做好初始化，普通 RNN 中用 relu 作為激活函數都是無妨的。

相關鏈接

[1]. Tian Qi C, Yulia R, Jesse B, David D. Neural Ordinary Differential Equations. arXiv preprint arXiv:1806.07366, 2018.

[2]. 兩生物種群競爭模型

https://kexue.fm/archives/3120

聲明：文章收集于網絡，如有侵權，請聯系小編及時處理，謝謝！

商業智能與數據分析群

興趣范圍包括各種讓數據產生價值的辦法，實際應用案例分享與討論，分析工具，ETL工具，數據倉庫，數據挖掘工具，報表系統等全方位知識

QQ群：81035754