資訊專欄INFORMATION COLUMN

摘要:要學習深度學習,那么首先要熟悉神經網絡,簡稱的一些基本概念。網絡徑向基函數網絡是一種單隱層前饋神經網絡,它使用徑向基函數作為隱層神經元激活函數,而輸出層則是對隱層神經元輸出的線性組合。
閱讀目錄
1. 神經元模型
2. 感知機和神經網絡
3. 誤差逆傳播算法
4. 常見的神經網絡模型
5. 深度學習
6. 參考內容

目前,深度學習(Deep Learning,簡稱DL)在算法領域可謂是大紅大紫,現在不只是互聯網、人工智能,生活中的各大領域都能反映出深度學習引領的巨大變革。要學習深度學習,那么首先要熟悉神經網絡(Neural Networks,簡稱NN)的一些基本概念。當然,這里所說的神經網絡不是生物學的神經網絡,我們將其稱之為人工神經網絡(Artificial Neural Networks,簡稱ANN)貌似更為合理。神經網絡最早是人工智能領域的一種算法或者說是模型,目前神經網絡已經發展成為一類多學科交叉的學科領域,它也隨著深度學習取得的進展重新受到重視和推崇。
為什么說是“重新”呢?其實,神經網絡更為一種算法模型很早就已經開始研究了,但是在取得一些進展后,神經網絡的研究陷入了一段很長時間的低潮期,后來隨著Hinton在深度學習上取得的進展,神經網絡又再次受到人們的重視。本文就以神經網絡為主,著重總結一些相關的基礎知識,然后在此基礎上引出深度學習的概念,如有書寫不當的地方,還請大家評批指正。
1. 神經元模型
神經元是神經網絡中最基本的結構,也可以說是神經網絡的基本單元,它的設計靈感完全來源于生物學上神經元的信息傳播機制。我們學過生物的同學都知道,神經元有兩種狀態:興奮和抑制。一般情況下,大多數的神經元是處于抑制狀態,但是一旦某個神經元收到刺激,導致它的電位超過一個閾值,那么這個神經元就會被激活,處于“興奮”狀態,進而向其他的神經元傳播化學物質(其實就是信息)。
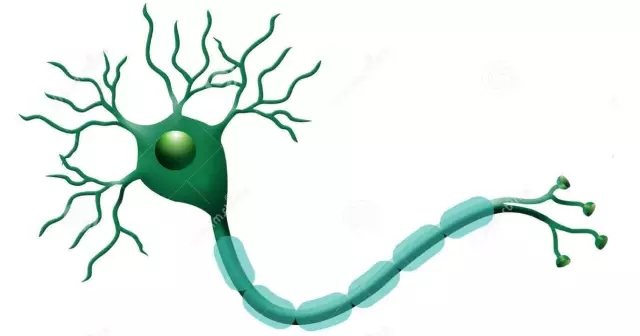
下圖為生物學上的神經元結構示意圖:
1943年,McCulloch和Pitts將上圖的神經元結構用一種簡單的模型進行了表示,構成了一種人工神經元模型,也就是我們現在經常用到的“M-P神經元模型”,如下圖所示:
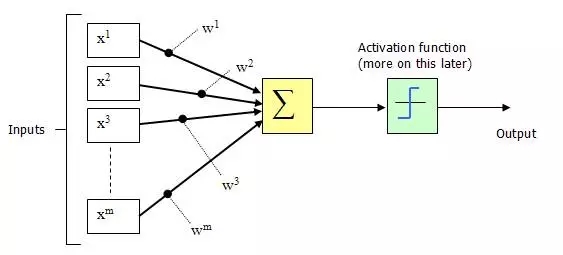
從上圖M-P神經元模型可以看出,神經元的輸出
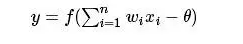
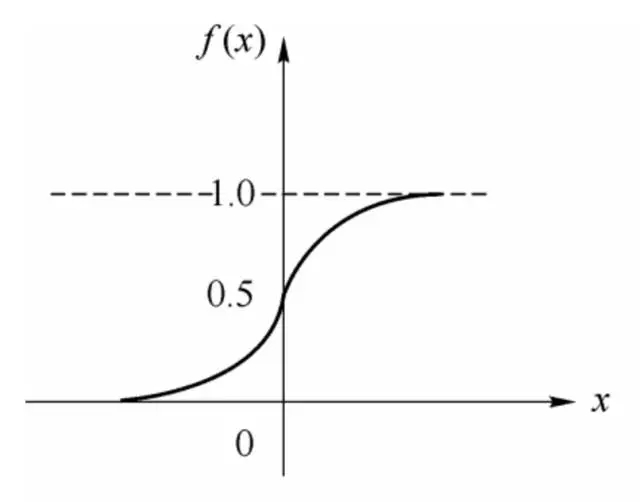
其中θ為我們之前提到的神經元的激活閾值,函數f(?)也被稱為是激活函數。如上圖所示,函數f(?)可以用一個階躍方程表示,大于閾值激活;否則則抑制。但是這樣有點太粗暴,因為階躍函數不光滑,不連續,不可導,因此我們更常用的方法是用sigmoid函數來表示函數函數f(?)。
sigmoid函數的表達式和分布圖如下所示:
2. 感知機和神經網絡
感知機(perceptron)是由兩層神經元組成的結構,輸入層用于接受外界輸入信號,輸出層(也被稱為是感知機的功能層)就是M-P神經元。下圖表示了一個輸入層具有三個神經元(分別表示為x0、x1、x2)的感知機結構:

根據上圖不難理解,感知機模型可以由如下公式表示:
? ? ? ? ? ? ? ? ? ? ? ? y=f(wx+b)
其中,w為感知機輸入層到輸出層連接的權重,b表示輸出層的偏置。事實上,感知機是一種判別式的線性分類模型,可以解決與、或、非這樣的簡單的線性可分(linearly separable)問題,線性可分問題的示意圖見下圖:
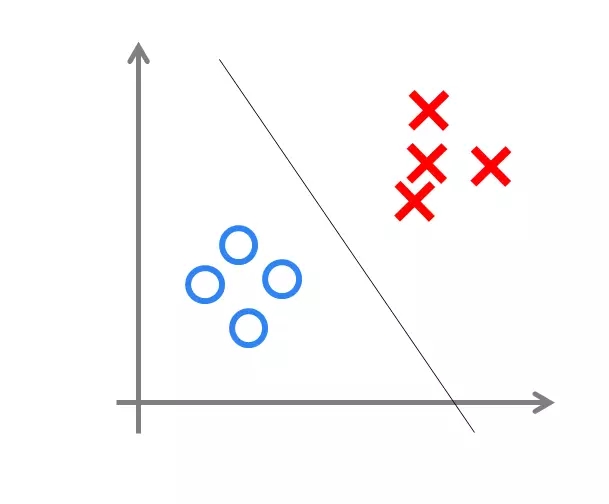
但是由于它只有一層功能神經元,所以學習能力非常有限。事實證明,單層感知機無法解決最簡單的非線性可分問題——異或問題。
關于感知機解決異或問題還有一段歷史值得我們簡單去了解一下:感知器只能做簡單的線性分類任務。但是當時的人們熱情太過于高漲,并沒有人清醒的認識到這點。于是,當人工智能領域的巨擘Minsky指出這點時,事態就發生了變化。Minsky在1969年出版了一本叫《Perceptron》的書,里面用詳細的數學證明了感知器的弱點,尤其是感知器對XOR(異或)這樣的簡單分類任務都無法解決。Minsky認為,如果將計算層增加到兩層,計算量則過大,而且沒有有效的學習算法。所以,他認為研究更深層的網絡是沒有價值的。由于Minsky的巨大影響力以及書中呈現的悲觀態度,讓很多學者和實驗室紛紛放棄了神經網絡的研究。神經網絡的研究陷入了冰河期。這個時期又被稱為“AI winter”。接近10年以后,對于兩層神經網絡的研究才帶來神經網絡的復蘇。
我們知道,我們日常生活中很多問題,甚至說大多數問題都不是線性可分問題,那我們要解決非線性可分問題該怎樣處理呢?這就是這部分我們要引出的“多層”的概念。既然單層感知機解決不了非線性問題,那我們就采用多層感知機,下圖就是一個兩層感知機解決異或問題的示意圖:
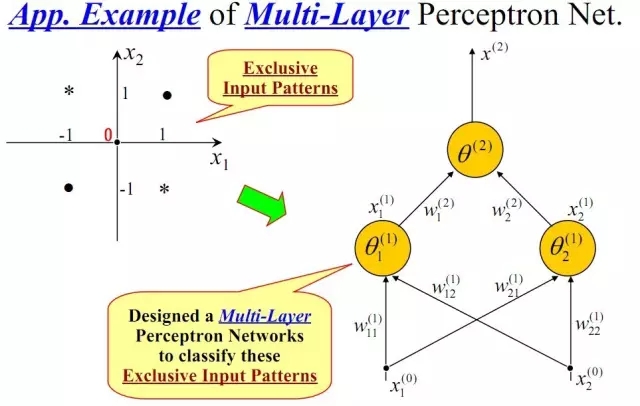
構建好上述網絡以后,通過訓練得到最后的分類面如下:
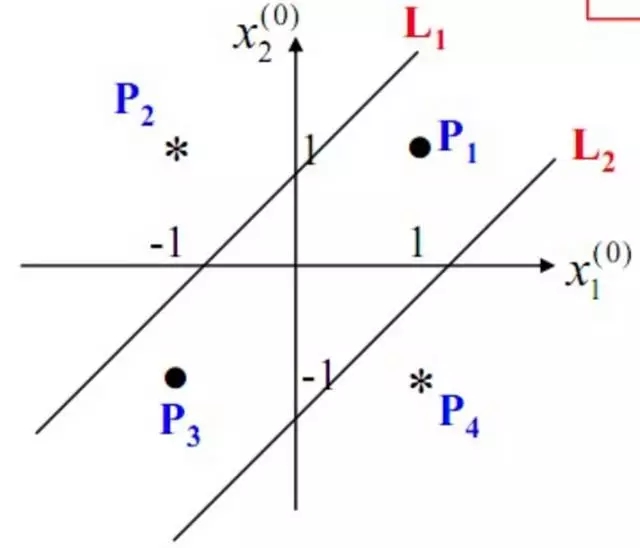
由此可見,多層感知機可以很好的解決非線性可分問題,我們通常將多層感知機這樣的多層結構稱之為是神經網絡。但是,正如Minsky之前所擔心的,多層感知機雖然可以在理論上可以解決非線性問題,但是實際生活中問題的復雜性要遠不止異或問題這么簡單,所以我們往往要構建多層網絡,而對于多層神經網絡采用什么樣的學習算法又是一項巨大的挑戰,如下圖所示的具有4層隱含層的網絡結構中至少有33個參數(不計偏置bias參數),我們應該如何去確定呢?
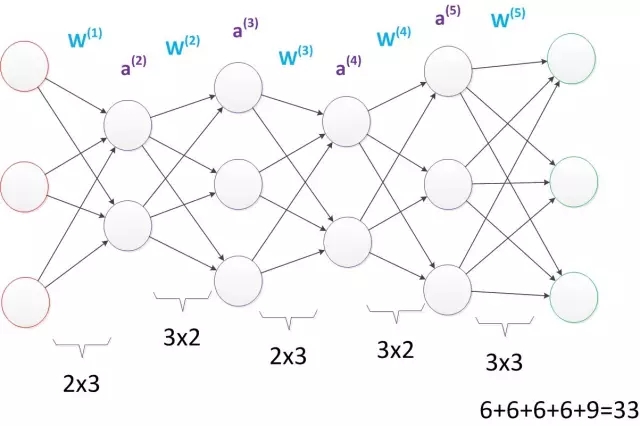
3. 誤差逆傳播算法
所謂神經網絡的訓練或者是學習,其主要目的在于通過學習算法得到神經網絡解決指定問題所需的參數,這里的參數包括各層神經元之間的連接權重以及偏置等。因為作為算法的設計者(我們),我們通常是根據實際問題來構造出網絡結構,參數的確定則需要神經網絡通過訓練樣本和學習算法來迭代找到最優參數組。
說起神經網絡的學習算法,不得不提其中最杰出、最成功的代表——誤差逆傳播(error BackPropagation,簡稱BP)算法。BP學習算法通常用在更為廣泛使用的多層前饋神經網絡中。

4. 常見的神經網絡模型
4.1 Boltzmann機和受限Boltzmann機
神經網絡中有一類模型是為網絡狀態定義一個“能量”,能量最小化時網絡達到理想狀態,而網絡的訓練就是在最小化這個能量函數。Boltzmann(玻爾茲曼)機就是基于能量的模型,其神經元分為兩層:顯層和隱層。顯層用于表示數據的輸入和輸出,隱層則被理解為數據的內在表達。Boltzmann機的神經元都是布爾型的,即只能取0、1值。標準的Boltzmann機是全連接的,也就是說各層內的神經元都是相互連接的,因此計算復雜度很高,而且難以用來解決實際問題。因此,我們經常使用一種特殊的Boltzmann機——受限玻爾茲曼機(Restricted Boltzmann Mechine,簡稱RBM),它層內無連接,層間有連接,可以看做是一個二部圖。下圖為Boltzmann機和RBM的結構示意圖:

RBM常常用對比散度(Constrastive Divergence,簡稱CD)來進行訓練。
4.2 RBF網絡
RBF(Radial Basis Function)徑向基函數網絡是一種單隱層前饋神經網絡,它使用徑向基函數作為隱層神經元激活函數,而輸出層則是對隱層神經元輸出的線性組合。下圖為一個RBF神經網絡示意圖:
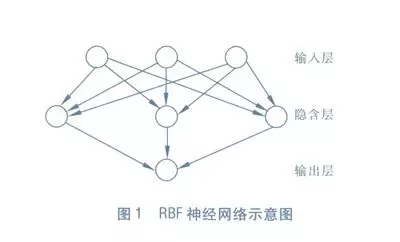
訓練RBF網絡通常采用兩步:
1> 確定神經元中心,常用的方式包括隨機采樣,聚類等;
2> 確定神經網絡參數,常用算法為BP算法。
4.3 ART網絡
ART(Adaptive Resonance Theory)自適應諧振理論網絡是競爭型學習的重要代表,該網絡由比較層、識別層、識別層閾值和重置模塊構成。ART比較好的緩解了競爭型學習中的“可塑性-穩定性窘境”(stability-plasticity dilemma),可塑性是指神經網絡要有學習新知識的能力,而穩定性則指的是神經網絡在學習新知識時要保持對舊知識的記憶。這就使得ART網絡具有一個很重要的優點:可進行增量學習或在線學習。
4.4 SOM網絡
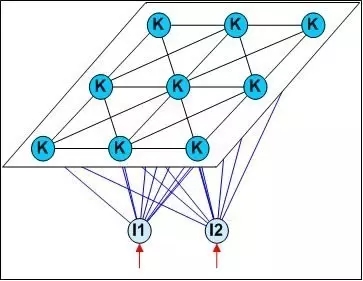
SOM(Self-Organizing Map,自組織映射)網絡是一種競爭學習型的無監督神經網絡,它能將高維輸入數據映射到低維空間(通常為二維),同事保持輸入數據在高維空間的拓撲結構,即將高維空間中相似的樣本點映射到網絡輸出層中的臨近神經元。下圖為SOM網絡的結構示意圖:
4.5 結構自適應網絡
我們前面提到過,一般的神經網絡都是先指定好網絡結構,訓練的目的是利用訓練樣本來確定合適的連接權、閾值等參數。與此不同的是,結構自適應網絡則將網絡結構也當做學習的目標之一,并希望在訓練過程中找到最符合數據特點的網絡結構。
4.6 遞歸神經網絡以及Elman網絡
與前饋神經網絡不同,遞歸神經網絡(Recurrent Neural Networks,簡稱RNN)允許網絡中出現環形結構,從而可以讓一些神經元的輸出反饋回來作為輸入信號,這樣的結構與信息反饋過程,使得網絡在tt時刻的輸出狀態不僅與tt時刻的輸入有關,還與t?1時刻的網絡狀態有關,從而能處理與時間有關的動態變化。
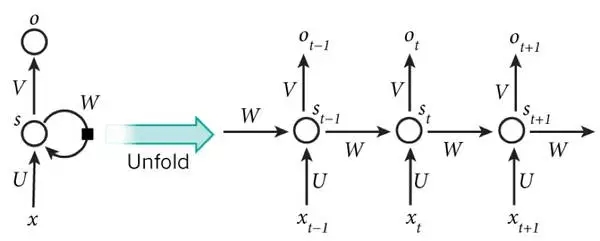
Elman網絡是最常用的遞歸神經網絡之一,其結構如下圖所示:

RNN一般的訓練算法采用推廣的BP算法。值得一提的是,RNN在(t+1)時刻網絡的結果O(t+1)是該時刻輸入和所有歷史共同作用的結果,這樣就達到了對時間序列建模的目的。因此,從某種意義上來講,RNN被視為是時間深度上的深度學習也未嘗不對。
RNN在(t+1)時刻網絡的結果O(t+1)是該時刻輸入和所有歷史共同作用的結果,這么講其實也不是很準確,因為“梯度發散”同樣也會發生在時間軸上,也就是說對于t時刻來說,它產生的梯度在時間軸上向歷史傳播幾層之后就消失了,根本無法影響太遙遠的過去。因此,“所有的歷史”只是理想的情況。在實際中,這種影響也就只能維持若干個時間戳而已。換句話說,后面時間步的錯誤信號,往往并不能回到足夠遠的過去,像更早的時間步一樣,去影響網絡,這使它很難以學習遠距離的影響。
為了解決上述時間軸上的梯度發散,機器學習領域發展出了長短時記憶單元(Long-Short Term Memory,簡稱LSTM),通過門的開關實現時間上的記憶功能,并防止梯度發散。其實除了學習歷史信息,RNN和LSTM還可以被設計成為雙向結構,即雙向RNN、雙向LSTM,同時利用歷史和未來的信息。
5. 深度學習
深度學習指的是深度神經網絡模型,一般指網絡層數在三層或者三層以上的神經網絡結構。
理論上而言,參數越多的模型復雜度越高,“容量”也就越大,也就意味著它能完成更復雜的學習任務。就像前面多層感知機帶給我們的啟示一樣,神經網絡的層數直接決定了它對現實的刻畫能力。但是在一般情況下,復雜模型的訓練效率低,易陷入過擬合,因此難以受到人們的青睞。具體來講就是,隨著神經網絡層數的加深,優化函數越來越容易陷入局部最優解(即過擬合,在訓練樣本上有很好的擬合效果,但是在測試集上效果很差)。同時,不可忽略的一個問題是隨著網絡層數增加,“梯度消失”(或者說是梯度發散diverge)現象更加嚴重。我們經常使用sigmoid函數作為隱含層的功能神經元,對于幅度為1的信號,在BP反向傳播梯度時,每傳遞一層,梯度衰減為原來的0.25。層數一多,梯度指數衰減后低層基本接收不到有效的訓練信號。
為了解決深層神經網絡的訓練問題,一種有效的手段是采取無監督逐層訓練(unsupervised layer-wise training),其基本思想是每次訓練一層隱節點,訓練時將上一層隱節點的輸出作為輸入,而本層隱節點的輸出作為下一層隱節點的輸入,這被稱之為“預訓練”(pre-training);在預訓練完成后,再對整個網絡進行“微調”(fine-tunning)訓練。比如Hinton在深度信念網絡(Deep Belief Networks,簡稱DBN)中,每層都是一個RBM,即整個網絡可以被視為是若干個RBM堆疊而成。在使用無監督訓練時,首先訓練第一層,這是關于訓練樣本的RBM模型,可按標準的RBM進行訓練;然后,將第一層預訓練號的隱節點視為第二層的輸入節點,對第二層進行預訓練;... 各層預訓練完成后,再利用BP算法對整個網絡進行訓練。
事實上,“預訓練+微調”的訓練方式可被視為是將大量參數分組,對每組先找到局部看起來較好的設置,然后再基于這些局部較優的結果聯合起來進行全局尋優。這樣就在利用了模型大量參數所提供的自由度的同時,有效地節省了訓練開銷。
另一種節省訓練開銷的做法是進行“權共享”(weight sharing),即讓一組神經元使用相同的連接權,這個策略在卷積神經網絡(Convolutional Neural Networks,簡稱CNN)中發揮了重要作用。下圖為一個CNN網絡示意圖:
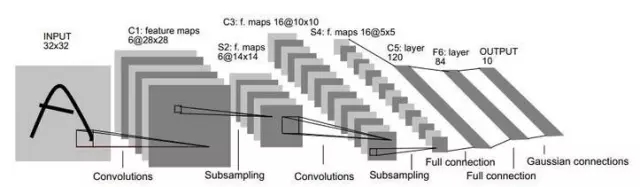
CNN可以用BP算法進行訓練,但是在訓練中,無論是卷積層還是采樣層,其每組神經元(即上圖中的每一個“平面”)都是用相同的連接權,從而大幅減少了需要訓練的參數數目。
6. 參考內容
1. 周志華《機器學習》
2. 知乎問答:http://www.zhihu.com/question/34681168
歡迎加入本站公開興趣群商業智能與數據分析群
興趣范圍包括各種讓數據產生價值的辦法,實際應用案例分享與討論,分析工具,ETL工具,數據倉庫,數據挖掘工具,報表系統等全方位知識
QQ群:81035754
文章版權歸作者所有,未經允許請勿轉載,若此文章存在違規行為,您可以聯系管理員刪除。
轉載請注明本文地址:http://m.specialneedsforspecialkids.com/yun/4356.html
摘要:近日,發布了其關于神經網絡可解釋性的研究成果,他們通過刪除網絡中的某些神經元組,從而判定其對于整個網絡是否重要。泛化性良好的網絡對于刪除神經元的操作更具適應性。通過刪除單個神經元和神經元組,我們測量了破壞網絡對性能的影響。 深度學習算法近年來取得了長足的進展,也給整個人工智能領域送上了風口。但深度學習系統中分類器和特征模塊都是自學習的,神經網絡的可解釋性成為困擾研究者的一個問題,人們常常將其...
摘要:較大池化一個卷積神經網絡的典型架構卷積神經網絡的典型架構我們已經討論過卷積層用表示和池化層用表示只是一個被應用的非線性特征,類似于神經網絡。 這是作者在 Medium 上介紹神經網絡系列文章中的一篇,他在這里詳細介紹了卷積神經網絡。卷積神經網絡在圖像識別、視頻識別、推薦系統以及自然語言處理中都有很廣的應用。如果想瀏覽該系列文章,可點擊閱讀原文查看原文網址。跟神經網絡一樣,卷積神經網絡由神經元...
閱讀 1534·2021-09-22 15:35
閱讀 2014·2021-09-14 18:04
閱讀 884·2019-08-30 15:55
閱讀 2456·2019-08-30 15:53
閱讀 2685·2019-08-30 12:45
閱讀 1208·2019-08-29 17:01
閱讀 2584·2019-08-29 15:30
閱讀 3521·2019-08-29 15:09