摘要：在這個問題強化學習里，我遇到過很多人，他們始終不相信我們能夠通過一套算法，從像素開始從頭學會玩游戲這太驚人了，我自己也曾經(jīng)這么想。基于像素的乒乓游戲乒乓游戲是研究簡單強化學習的一個非常好的例子。

這是一篇早就應(yīng)該寫的關(guān)于強化學習的文章。強化學習現(xiàn)在很火！你可能已經(jīng)注意到計算機現(xiàn)在可以自動（從游戲畫面的像素中）學會玩雅達利（Atari）游戲[1]，它們已經(jīng)擊敗了圍棋界的世界冠軍，四足機器人學會了奔跑和跳躍，機器人正在學習如何執(zhí)行復(fù)雜的操作任務(wù)而無需顯式對其編程。所有的這些進步都源自強化學習研究的進展。我自己在過去一年里對強化學習產(chǎn)生了興趣，我讀完了Richard Sutton的書、David Silver的課程，瀏覽了John Schulmann的講義，在DeepMind實習的那個暑假里寫了一個Javascript的強化學習庫，并且最近也參與了OpenAI Gym項目的設(shè)計與開發(fā)。所以，我在強化學習這駕充滿樂趣的“馬車”上已經(jīng)待了至少一年的時間，但是直到現(xiàn)在，我才抽出時間來寫一寫為什么強化學習那么重要，它是關(guān)于什么，如何發(fā)展起來，未來可能走向何方？

我想從強化學習近幾年的進展出發(fā)，分析四個推進AI發(fā)展的關(guān)鍵因素：

計算（摩爾定律、GPU, ASIC）

數(shù)據(jù)（良構(gòu)數(shù)據(jù)，如：ImageNet）

算法（研究與想法，如：反向傳播、卷積網(wǎng)絡(luò)、LSTM），以及

基礎(chǔ)架構(gòu)（Linux, TCP/IP, Git, ROS, PR2, AWS, AMT, TensorFlow, etc.）

與計算機視覺的情境相似，強化學習的進展并不是由于出現(xiàn)了新的天才的想法。在計算機視覺研究中，2012年的AlexNet很大程度上只是1990年ConvNets的一個擴展（更深、更寬）。類似的，2013年ATARI Deep Q-Learning的文章只是標準Q-Learning算法的一個實現(xiàn)，區(qū)別在于它將ConvNet作為函數(shù)逼近子（function approximator）。AlphaGo使用的是策略梯度（policy gradient）以及蒙特卡洛樹搜索（MCTS）——這些都是標準且已有的技術(shù)。當然，我們需要很多技巧以及耐心來讓它變得有效，并在這些“古老”的算法上進行一些巧妙的調(diào)整和變化。但是給強化學習研究帶來進展的最直接原因并不是新的算法，而是計算能力、數(shù)據(jù)以及基礎(chǔ)架構(gòu)。

現(xiàn)在回到強化學習。每當遇到一些看似神奇而實則簡單的事情時，我都會感到坐立不安并想為它寫一篇文章。在這個問題（強化學習）里，我遇到過很多人，他們始終不相信我們能夠通過一套算法，從像素開始從頭學會玩ATARI游戲——這太驚人了，我自己也曾經(jīng)這么想。但是我們所使用的方法本質(zhì)上確實非常簡單（我承認當事后諸葛很容易）。盡管如此，我將為大家介紹我們在解決強化學習問題中最喜歡用的方法——策略梯度（Policy Gradient, PG）。假如你是一個強化學習的門外漢，你可能會好奇為什么我不介紹一種更為人所知的強化學習算法——DQN（深度Q-網(wǎng)絡(luò)），也就是那篇ATARI游戲的論文（來自DeepMind）中所采用的方法。實際上Q-Learning并不是一個非常棒的算法，大部分人更親睞使用策略梯度，就連原始DQN論文的作者也證明了策略梯度能夠比Q-Learning取得更好的結(jié)果。策略梯度的優(yōu)勢在于它是端到端（end-to-end）的：存在一個顯式的策略以及方法用來直接優(yōu)化期望回報（expected reward）。總之，我們將以乒乓游戲（Pong）為例，來介紹如何使用策略梯度，在深度神經(jīng)網(wǎng)絡(luò)的幫助下基于游戲畫面的像素來學會玩這個游戲。完整的實現(xiàn)只有130行Python代碼（使用Numpy）。讓我們開始吧。

基于像素的乒乓游戲

乒乓游戲是研究簡單強化學習的一個非常好的例子。在ATARI 2600中，我們將讓你控制其中一個球拍，另一個球拍則由AI控制。游戲是這么工作的：我們獲得一幀圖像（210*160*3的字節(jié)數(shù)組），然后決定將球拍往上還是往下移動（2種選擇）。每次選擇之后，游戲模擬器會執(zhí)行相應(yīng)的動作并返回一個回報（得分）：可能是一個+1（如果對方?jīng)]有接住球），或者-1（我們沒有接住球），或者為0（其他情況）。當然，我們的目標是移動球拍，使得我們的得分盡可能高。

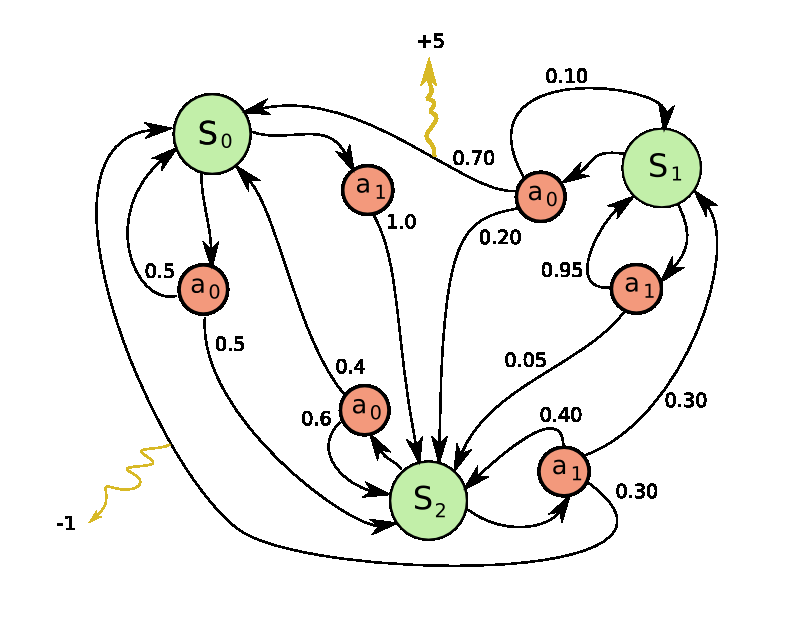
當我們描述解決方案的時候，請記住我們會盡量減少對于乒乓游戲本身的假設(shè)。因為我們更關(guān)心復(fù)雜、高維的問題，比如機器人操作、裝配以及導航。乒乓游戲只是一個非常簡單的測試用例，當我們學會它的同時，也將了解如何寫一個能夠完成任何實際任務(wù)的通用AI系統(tǒng)。

策略網(wǎng)絡(luò)

首先，我們將定義一個策略網(wǎng)絡(luò)，用于實現(xiàn)我們的玩家（智能體）。該網(wǎng)絡(luò)根據(jù)當前游戲的狀態(tài)來判斷應(yīng)該執(zhí)行的動作（上移或者下移）。簡單起見，我們使用一個2層的神經(jīng)網(wǎng)絡(luò)，以當前游戲畫面的像素（100,800維，210*160*3）作為輸入，輸出一個多帶帶的值表示“上移”動作的概率。在每輪迭代中，我們會根據(jù)該分布進行采樣，得到實際執(zhí)行的動作。這么做的原因會在接下來介紹訓練過程的時候更加清楚。

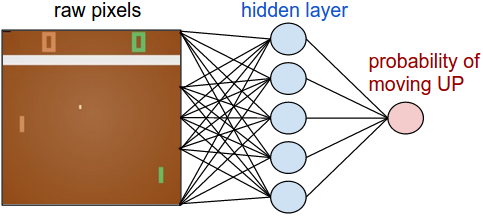
我們將它具體化，下面是我們?nèi)绾问褂肞ython/numpy來實現(xiàn)該策略網(wǎng)絡(luò)。假設(shè)輸入為x，即（預(yù)處理過的）像素信息：

h = np.dot(W1, x) # compute hidden layer neuron activations

h[h<0] = 0 # ReLU nonlinearity: threshold at zero

logp = np.dot(W2, h) # compute log probability of going up

p = 1.0 / (1.0 + np.exp(-logp)) # sigmoid function (gives probability of going up)

在這段簡短的代碼中，W1與W2是兩個隨機初始化的權(quán)值矩陣。我們使用sigmoid函數(shù)作為非線性激活函數(shù)，以獲得概率值（[0,1]）。直覺上，隱含層神經(jīng)元會檢測游戲的當前狀態(tài)（比如：球與球拍的位置），而W2則根據(jù)隱含層狀態(tài)來決定當前應(yīng)該執(zhí)行的動作。因此，W1與W2將成為決定我們玩家水平的關(guān)鍵因素。

補充：之所以提到預(yù)處理，是因為我們通常需要2幀以上的畫面作為策略網(wǎng)絡(luò)的輸入，這樣策略網(wǎng)絡(luò)才能夠檢測當前球的運動狀態(tài)。由于我是在自己的Macbook上進行實驗的，所以我只考慮非常簡單的預(yù)處理：實際上我們將當前幀與上一幀畫面的差作為輸入。

這聽起來并不現(xiàn)實

我想你已經(jīng)體會到這個任務(wù)的難度。每一步，我們?nèi)〉?00,800個值作為輸入，并傳遞給策略網(wǎng)絡(luò)（W1、W2的參數(shù)數(shù)目將為百萬級別）。假設(shè)我們決定往上移動球拍，當前的游戲可能給我們反饋的回報是0，并呈現(xiàn)下一幀畫面（同樣是100,800個值）。我們重復(fù)這個過程上百次，最終得到一個非零的回報（得分）。假設(shè)我們最后得到的回報是+1，非常棒，但是我們?nèi)绾沃磊A在哪一步呢？是取得勝利之前的那一步？還是在76步之前？又或許，它和第10步與第90步有關(guān)？同時，我們又該更新哪些參數(shù)，如何更新，使得它在未來能夠做得更好？我們將它稱之為信用分配問題（credit assignment）。在乒乓游戲的例子里，當對方?jīng)]有接住球的時候，我們會得到+1的回報。其直接原因是我們恰好將球以一個巧妙的軌跡彈出，但實際上，我們在很多步之前就已經(jīng)這么做了，只不過那之后的所有動作都不直接導致我們結(jié)束游戲并獲得回報。由此可見，我們正面臨一個多么困難的問題。

有監(jiān)督學習

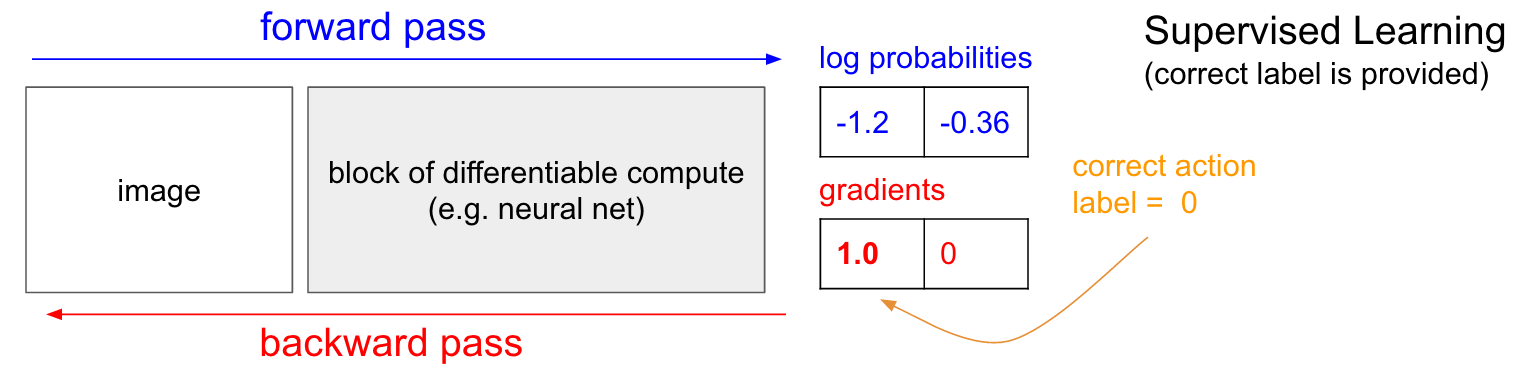
在我們深入介紹策略梯度之前，我想簡單回顧一下有監(jiān)督學習（supervised learning），因為我們將會看到，強化學習與之很相似。參考下圖。在一般的有監(jiān)督學習中，我們將一幅圖片作為網(wǎng)絡(luò)的輸入，并獲得某種概率分布，如：上移（UP）與下移（DOWN）兩個類別。在這個例子中，我給出了這兩種類別的對數(shù)概率（log probabilities）（-1.2, -0.36）（我們沒有列出原始的概率：0.3/0.7，因為我們始終是以正確類別的對數(shù)似然作為優(yōu)化目標的）。在有監(jiān)督學習中，我們已經(jīng)知道每一步應(yīng)該執(zhí)行的動作。假設(shè)當前狀態(tài)下，正確的動作是往上移（label 0）。那么在實現(xiàn)時，我們會先給UP的對數(shù)概率一個1.0的梯度，然后執(zhí)行反向傳播計算梯度向量。梯度值將指導我們?nèi)绾胃孪鄳?yīng)的參數(shù)，使得網(wǎng)絡(luò)更傾向于預(yù)測UP這個動作。當我們更新參數(shù)之后，我們的網(wǎng)絡(luò)將在未來遇到相似輸入畫面時更傾向預(yù)測UP動作。

策略梯度

但是，在強化學習中我們并沒有正確的標簽信息，又該怎么做呢？下面介紹策略梯度方法。我們的策略網(wǎng)絡(luò)預(yù)測上移（UP）的概率為30%，下移（DOWN）的概率為70%。我們將根據(jù)該分布采樣出一個動作（如DOWN）并執(zhí)行。注意到一個有趣的事實，我們可以像在有監(jiān)督學習中所做的，立刻給DOWN一個梯度1.0，再進行反向傳播更新網(wǎng)絡(luò)參數(shù)，使得網(wǎng)絡(luò)在未來更傾向預(yù)測DOWN。然而問題是，在當前狀態(tài)下，我們并不知道DOWN是一個好的動作。但是沒關(guān)系，我們可以等著瞧！比如在乒乓游戲中，我們可以等到游戲結(jié)束，獲得游戲的回報（勝：+1；負：-1），再對我們所執(zhí)行過的動作賦予梯度（DOWN）。在下面這個例子中，下移（DOWN）的后果是導致我們輸了游戲（回報為-1），因此我們給DOWN的對數(shù)概率-1的梯度，再執(zhí)行反向傳播，使得網(wǎng)絡(luò)在遇到相似輸入的時候預(yù)測DOWN的概率降低。

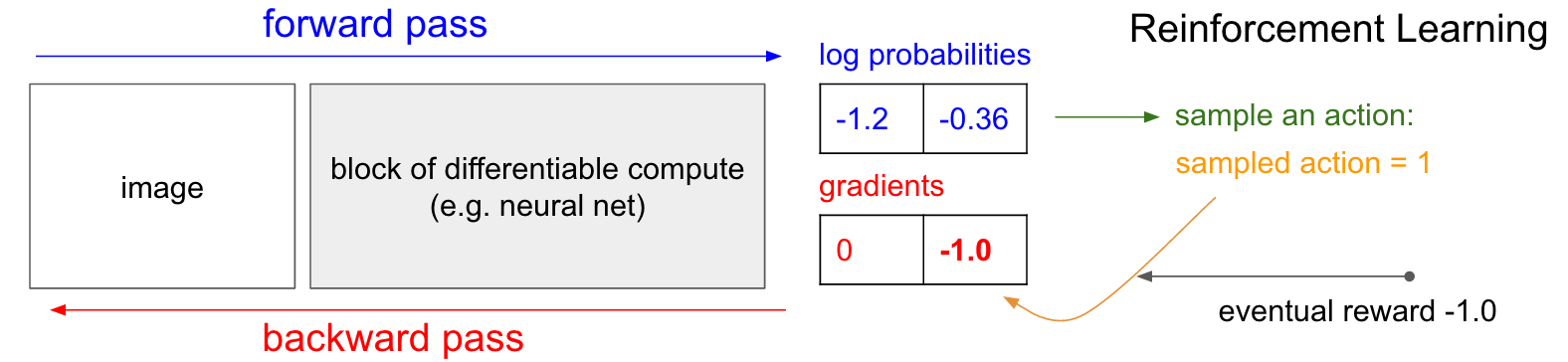
就這么簡單。我們有一個隨機的策略對動作進行采樣，對于那些最終能夠帶來勝利的動作進行激勵，而抑制那些最終導致游戲失敗的動作。同時，回報并不限制為+1/-1，它可以是任何度量。假如確實贏得漂亮，回報可以為10.0，我們將該回報值寫進梯度再進行反向傳播。這就是神經(jīng)網(wǎng)絡(luò)的美妙之處，使用它們的時候就像是一種騙術(shù)，你能夠?qū)Π偃f個參數(shù)執(zhí)行萬億次浮點運算，用SGD來讓它做任何事情。它本不該行得通，但有趣的是，在我們生活的這個宇宙里，它確實是有效的。

訓練準則

接下來，我們詳細介紹訓練過程。我們首先對策略網(wǎng)絡(luò)中的W1, W2進行初始化，然后玩100局乒乓游戲（我們把最初的策略稱為rollouts）。假設(shè)每一次游戲包含200幀畫面，那么我們一共作了20,000次UP/DOWN的決策，而且對于每一次決策，我們知道當前參數(shù)的梯度。剩下的工作就是為每個決策標注出其“好”或“壞”。假設(shè)我們贏了12局，輸了88局，那么我們將對于那些勝局中200*12=2400個決策進行正向更新（positive update，為相應(yīng)的動作賦予+1.0的梯度，并反向傳播，更新參數(shù)）；而對敗局中200*88=17600個決策進行負向更新。是的，就這么簡單。更新完成之后的策略網(wǎng)絡(luò)將會更傾向執(zhí)行那些能夠帶來勝利的動作。于是，我們可以使用改進之后的策略網(wǎng)絡(luò)再玩100局，循環(huán)往復(fù)。

策略梯度：對于一個策略執(zhí)行多次，觀察哪些動作會帶來高回報，提高執(zhí)行它們的概率。

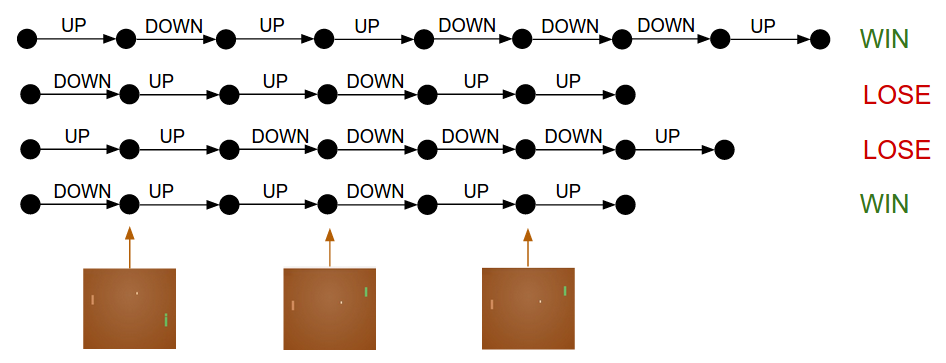
如果你仔細思考這個過程，你會發(fā)現(xiàn)一些有趣的性質(zhì)。比如，當我們在第50幀的時候作了一個好的動作（正確地回球），但是在第150幀沒有接住球，將會如何？按照我們所描述的做法，這一局中所有動作都將被標記為“壞”的動作（因為我們輸了），而這樣不是也否定了我們在第50幀時所作出的正確決策么？你是對的——它會這樣做。然而，如果你考慮上百萬次游戲過程，一個正確的動作給你帶來勝利的概率仍然是更大的，也就意味著你將會觀察到更多的正向更新，從而使得你的策略依然會朝著正確的方向改進。

更一般的回報函數(shù)

到目前為止，我們都是通過是否贏得游戲來判斷每一步?jīng)Q策的好壞。在更一般的強化學習框架中，我們可能在每一步?jīng)Q策時都會獲得一些回報rt。一個常見的選擇是采用有折扣的回報（discounted reward），這樣一來，“最終回報”則為: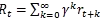，其中γ為折扣因子（0到1之間）。這意味著對于每一步所采樣的動作，我們考慮未來所有回報的加權(quán)和，而且未來回報的重要性隨時間以指數(shù)遞減。在實際中，對回報值進行規(guī)范化也很重要。比如，當我們算完100局乒乓游戲中20,000個動作的回報Rt之后，一個好的做法是先對這些回報值進行規(guī)范化（standardize，如減去均值，除標準差）再進行反向傳播。這樣一來，被激勵以及被抑制的動作大概各占一半。從數(shù)學角度，我們可以將這種做法看成是一種控制策略梯度估計方差的一種方法。更深入的探討請參考論文：High-Dimensional Continuous Control Using Generalized Advantage Estimation。

策略梯度的推導

接下來，我將從數(shù)學角度簡要介紹策略梯度的推導過程。策略梯度是值函數(shù)梯度估計的一個特例。更一般的情況下，表達式滿足這樣的形式: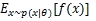，即某個值函數(shù)f(x)在概率分布p(x;θ)下的期望。提示：f(x)將是我們的回報函數(shù)（或者advantage function），而p(x)是我們的策略網(wǎng)絡(luò)，實際上是p(a|I)，即在給定圖像I的條件下，動作的概率分布。我們感興趣的是如何調(diào)整該分布（通過它的參數(shù)θ）以提高樣本的期望回報。

首先，我們有一個用以動作采樣的分布p(x;θ)（比如，可以是一個高斯分布）。對于每一個采樣，我們通過估值函數(shù)f對其進行打分。上面的式子告訴我們?nèi)绾胃逻@個分布，使得我們所采樣的動作能夠獲得更高的分數(shù)。更具體一點，我們采樣出一些樣本（動作）x，獲得它們的得分f(x)，同時對于x中的每一個樣本計算式中的第二項：。這一項代表什么含義？它是一個向量，指向能夠使得樣本x 概率增加的參數(shù)更新方向。回到上面的式子，最終的梯度是該向量與樣本得分f(x)的乘積，從而使得得分更高的樣本比得分較低的樣本對分布p(x;θ)的影響更大。

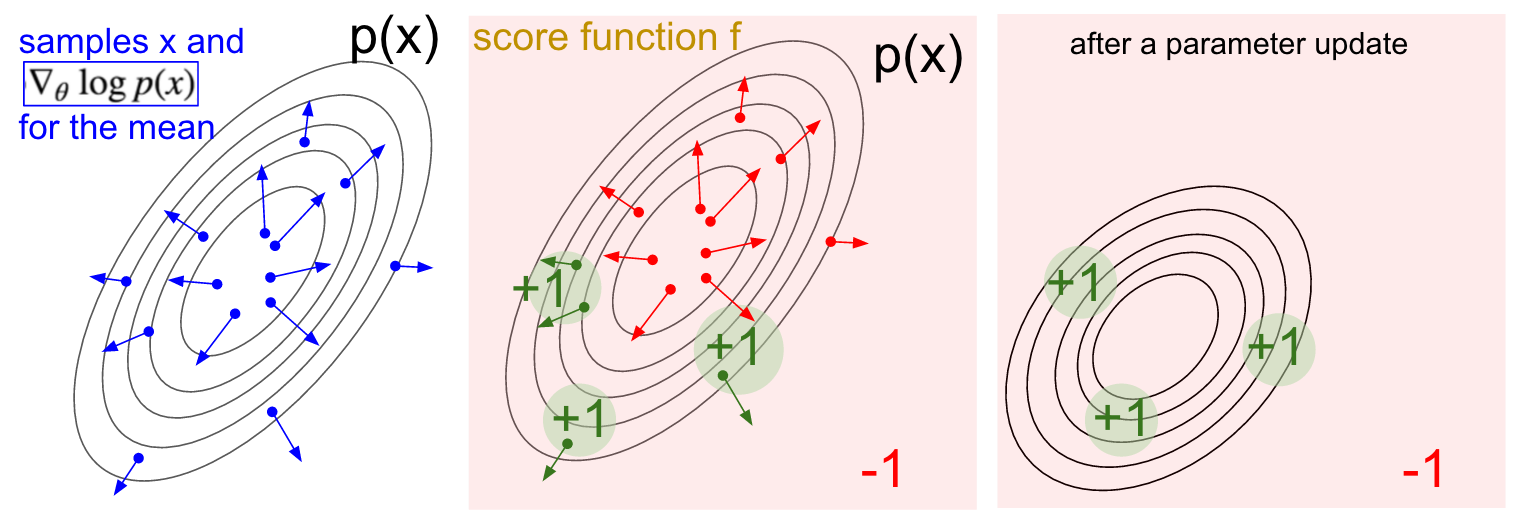
我希望策略網(wǎng)絡(luò)與強化學習之間的聯(lián)系已經(jīng)介紹清楚了。策略網(wǎng)絡(luò)為我們提供一些動作的樣本，并且其中一些動作比另外一些得分（由估值函數(shù)給出）更高。這部分所談及的數(shù)學部分則指導我們?nèi)绾胃虏呗跃W(wǎng)絡(luò)的參數(shù)：計算相應(yīng)動作的梯度，乘上它的得分，再更新網(wǎng)絡(luò)參數(shù)。一個更全面的推導過程以及討論，推薦大家看看John Sculman的講座。

學習

好，我們已經(jīng)了解了策略梯度以及它的推導過程。我在OpenAI Gym項目中ATARI 2600 Pong的基礎(chǔ)之上實現(xiàn)了整個方法，一共是130行Python代碼。我訓練了一個兩層的策略網(wǎng)絡(luò)，隱層200個神經(jīng)元，使用RMSProp算法更新參數(shù)。我沒有進行太多地調(diào)參（超參），實驗在我的Macbook上跑的。在訓練了3晚上之后，我得到了一個比AI玩家稍好的策略。這個算法大概模擬了200,000局游戲，執(zhí)行了800次左右參數(shù)更新。我朋友告訴我，如果使用ConvNet在GPU上跑幾天的話，你的勝率會更高。而如果你再優(yōu)化一下超參數(shù)，你就可以完勝每一局游戲。但是我在這篇文章里只是為了展示核心的思想，并沒有花太多時間去調(diào)整模型，所以最終得到的只是一個表現(xiàn)還不錯的乒乓游戲AI。

學到的（網(wǎng)絡(luò)）權(quán)重

我們來觀察一下所學到的網(wǎng)絡(luò)權(quán)重（weights）。經(jīng)預(yù)處理之后，網(wǎng)絡(luò)的輸入是一個80*80的差值圖像（當前幀減去上一幀，以反映圖像變化軌跡）。我們將W1按行進行展開（每一行的維度則為80*80）并可視化。下面展示了200個隱層神經(jīng)元中的40個。白色像素表示權(quán)值為正，黑色為負。可以看到，有一些神經(jīng)元顯示了球的運動軌跡（黑白相間的線條）。由于每個時刻球只能處在一個位置，所以這些神經(jīng)元實際上在進行多任務(wù)處理（multitasking），并在球出現(xiàn)在相應(yīng)位置時被充分激活。當球沿著相應(yīng)的軌跡運動時，該神經(jīng)元的響應(yīng)將呈現(xiàn)出正弦波形的波動，而由于ReLU的影響，它只會在一些離散的位置被激活。畫面中有一些噪聲，我想可以通過L2正則來消解。

What isn’t happening

策略梯度算法是以一種巧妙的“guess-and-check”模式工作的，“guess”指的是我們每一次都根據(jù)當前策略來對動作進行采樣，“check”指的是我們不斷激勵那些能夠帶來好運（贏或者得分更高）的動作。這種算法是目前解決強化學習問題較好的方法，但是一旦你理解了它的工作方式，你多少會感到有點失望，并心生疑問——它在什么情況下會失效呢？

與人類學習玩乒乓游戲的方式相比，我們需要注意以下區(qū)別：

在實際場景中，人類通常以某種方式（比如：英語）對這個任務(wù)進行交流，但是在一個標準的強化學習問題中，我們只有與環(huán)境交互而產(chǎn)生的回報。假如人類在對回報函數(shù)一無所知的情況下學習玩這個游戲（尤其是當回報函數(shù)是某種靜態(tài)但是隨機的函數(shù)），那么他也許會遇到非常多的困難，而此時策略梯度的方法則會有效得多。類似的，假如我們把每一幀畫面隨機打亂，那么人類很可能會輸?shù)粲螒颍鴮τ诓呗蕴荻确▍s不會有什么影響。

人類有豐富的先驗知識，比如物理相關(guān)（球的反彈，它不會瞬移，也不會忽然停止，它是勻速運動，等）與心理直覺。而且你也知道球拍是由你控制的，會對你的“上移/下移”指令作出回應(yīng)。而我們的算法則是完全從一無所知的狀態(tài)開始學習。

策略梯度是一種brute force（暴力搜索）算法。正確的動作最終會被發(fā)現(xiàn)并被內(nèi)化至策略當中。人類則會構(gòu)建一個強大的抽象模型，并根據(jù)它來作出規(guī)劃。在乒乓游戲里，我能夠推斷出對手速度很慢，因此將球快速擊出可能是一個好的策略。然而，似乎我們最終同樣會把這些好的策略內(nèi)化至我們的肌肉記憶，從而作出反射式操作。比如，當我們在學習開手動檔車的時候，你會發(fā)現(xiàn)自己在一開始需要很多思考，但是最終會成為一種自動而下意識的操作。

采用策略梯度時需要不斷地從正回報樣本中進行學習，從而調(diào)整參數(shù)。而在人類進行學習的過程中，即使沒有經(jīng)歷過相應(yīng)的選擇（樣本），也能夠判斷出哪個動作會有較高的回報。比如，我并不需要上百次的撞墻經(jīng)歷才能夠?qū)W會在開車時如何避免（撞墻）。

綜上所述，一旦你理解了這些算法工作的原理，你就可以推斷出它們的優(yōu)勢以及不足。特別地，我們離像人類一樣通過構(gòu)建抽象而豐富的游戲表示以進行快速地規(guī)劃和學習還差得很遠。未來的某天，計算機將會從一組像素中觀察到一把鑰匙和一扇門，并且會想要拿起鑰匙去開門。目前為止，我們離這個目標還有很長的距離，而且這也是相關(guān)研究的熱點領(lǐng)域。

神經(jīng)網(wǎng)絡(luò)中的不可微計算

這一節(jié)將討論策略梯度的另一個有趣的應(yīng)用，與游戲無關(guān)：它允許我們設(shè)計、訓練含有不可微計算的神經(jīng)網(wǎng)絡(luò)。這種思想最早在論文“Recurrent Models of visual Attention”中提出。這篇論文主要研究低分辨率圖像序列的處理。在每一輪迭代中，RNN會接收圖片的某一部分作為輸入，然后采樣出下個區(qū)域的位置。例如，RNN可能先看到（5, 30）這個位置，獲得該區(qū)域的圖片信息，然后決定接下來看（24, 50）這個位置。這種方法的關(guān)鍵在于從當前圖片（局部）中產(chǎn)生下一個觀察位置的概率分布并進行采樣。不幸地是，這個操作是不可微的。更一般地，我們考慮下面的神經(jīng)網(wǎng)絡(luò)：

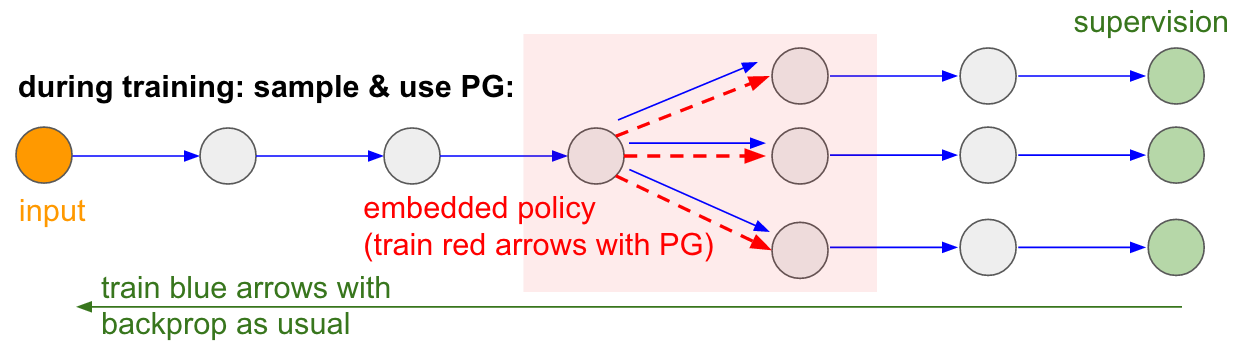
注意到大部分箭頭（藍色）是連續(xù)可微的，但是其中某些過程可能會包含不可微的采樣操作（紅色）。對于藍箭頭我們可以輕易地進行反向傳播，而對于紅色箭頭則不能。

使用策略梯度可以解決這個問題！我們將網(wǎng)絡(luò)中的采樣過程視為嵌入在網(wǎng)絡(luò)中的一個隨機策略。那么，在訓練時，我們將產(chǎn)生不同的樣本（下圖中的分支），然后我們在參數(shù)更新過程中對那些最終能夠得到好結(jié)果（最終的loss小）的采樣進行激勵。換言之，對于藍色箭頭上的參數(shù)，我們依然按照一般的反向傳播來更新；而對于紅色箭頭上的參數(shù)，我們采用策略梯度法更新。論文：Gradient Estimation Using Stochastic Computation Graphs對這種思路作了很好地形式化描述。

可訓練的記憶讀寫。你會在很多其他論文中看到這種想法，例如：Neural Turing Machine（NTM）有一個可讀寫的存儲帶。在執(zhí)行寫操作時，我們可能執(zhí)行的是類似m[i]=x的操作，其中i和x是由RNN控制器預(yù)測的。但是這個操作并不可微，因為我們并不知道如果我們寫的是一個不同的位置 j!=i 時loss會有什么樣的變化。因此，NTM只好執(zhí)行一種“軟”的讀/寫操作：它首先預(yù)測一個注意力的分布（attention distribution）a（按可寫的位置進行歸一化），然后執(zhí)行：for all i: m[i] = a[i]*x。是的，這樣做的確可微了，但是計算代價也高了很多。想象一下，我們每次賦值都需要訪問整個內(nèi)存空間！

然而，我們可以使用策略梯度來避免這個問題（理論上），正如RL-NTM所做的（arxiv.org/abs/1505.00521）。我們?nèi)匀活A(yù)測一個注意力的分布 a，再根據(jù)a ?對將要寫的地址 i 進行采樣：i = sample(a); m[i] = x。在訓練過程中，我們會對 i 采樣多次，并通過策略梯度法來對那些較好的采樣進行激勵。這樣一來，在預(yù)測時就只需要對一個位置進行讀/寫操作了。但是，正如這篇文章（RL-NTM）所指出的，策略梯度算法更適用于采樣空間較小的情況，而在這種搜索空間巨大的任務(wù)中，策略梯度并不是很有效。

結(jié)論

我們已經(jīng)看到策略梯度是一種強大且通用的算法。我們以ATARI 乒乓游戲為例，使用130行Python代碼訓練得到了一個智能體。同樣的算法也適用于其他的任何游戲，甚至在未來可用于有實際價值的控制問題。在擲筆之前，我想再補充一些說明：

關(guān)于推進人工智能。我們看到策略梯度算法是通過一個brute-force搜索的過程來完成的。我們同樣看到人類用以解決同樣問題的方法截然不同。正是由于人類所使用的那些抽象模型非常難以（甚至不可能）進行顯式地標注，所以最近越來越多的學者對于（無指導）生成模型（generative models）以及程序歸納（program induction）產(chǎn)生了興趣。

在復(fù)雜機器人場景中的應(yīng)用。將策略梯度算法應(yīng)用到搜索空間巨大的場景中并非易事，比如機器人控制（一個或多個機器人實時與現(xiàn)實世界進行交互）。解決這個問題的一個相關(guān)研究思路是：確定性的策略梯度（deterministic policy gradients），這種方法采用一個確定性的策略，并從一個額外的估值網(wǎng)絡(luò)（稱為critic）中獲取梯度信息。另一種思路是增加額外的指導。在很多實際的情形中，我們能夠從人類玩家那兒獲取一些專業(yè)的指導信息。比如AlphaGo先是根據(jù)人類玩家的棋譜，使用有監(jiān)督學習得到能夠較好地預(yù)測人類落子方式的策略，然后再使用策略梯度算法對此策略進行調(diào)整。

策略梯度在實際中的使用。在我之前關(guān)于RNN的博文中，我可能已經(jīng)讓大家看到了RNN的魔力。而事實上讓這些模型有效地工作是需要很多小技巧（trick）支撐的。策略梯度法也是如此。它是自動的，你需要大量的樣本，它可以一直學下去，當它效果不好的時候卻很難調(diào)試。無論什么時候，當我們使用火箭炮之前必須先試試空氣槍。以強化學習為例，我們在任何時候都需要首先嘗試的一個（強）基線系統(tǒng)是：交叉熵。假如你堅持要在你的問題中使用策略梯度，請一定要注意那些論文中所提到的小技巧，從簡單的開始，并使用策略梯度的的一種變型：TRPO。TRPO在實際應(yīng)用中幾乎總是優(yōu)于基本的策略梯度方法。其核心思想是通過引入舊策略和更新之后策略所預(yù)測的概率分布之間的KL距離，來控制參數(shù)更新的過程。

譯者：郭江 (哈工大 SCIR)

商業(yè)智能與數(shù)據(jù)分析群

興趣范圍包括各種讓數(shù)據(jù)產(chǎn)生價值的辦法，實際應(yīng)用案例分享與討論，分析工具，ETL工具，數(shù)據(jù)倉庫，數(shù)據(jù)挖掘工具，報表系統(tǒng)等全方位知識

QQ群：81035754