資訊專欄INFORMATION COLUMN

摘要:循環神經網絡令語音和自然語言處理達到了新階段。自歸一化神經網絡對于擾動是具有魯棒性的,它在訓練誤差上并沒有高方差見圖。構建自歸一化神經網絡我們通過調整函數的屬性以構建自歸一化神經網絡。
近日,arXiv 上公開的一篇 NIPS 投稿論文《Self-Normalizing Neural Networks》引起了圈內極大的關注,它提出了縮放指數型線性單元(SELU)而引進了自歸一化屬性,該單元主要使用一個函數 g 映射前后兩層神經網絡的均值和方差以達到歸一化的效果。該論文的作者為 Sepp Hochreiter,也就是當年和 Jürgen Schmidhuber 一起發明 LSTM 的大牛,之前的 ELU 同樣來自于他們組。有趣的是,這篇 NIPS 投稿論文雖然只有 9 頁正文,卻有著如同下圖一樣的 93 頁證明附錄。

在這篇文章中,機器之心對該論文進行了概要介紹。此外,Github 上已有人做出了論文中提出的 SELUs 與 ReLU 和 Leaky ReLU 的對比,我們也對此對比進行了介紹。

論文地址:https://arxiv.org/pdf/1706.02515.pdf
摘要:深度學習不僅通過卷積神經網絡(CNN)變革了計算機視覺,同時還通過循環神經網絡(RNN)變革了自然語言處理。然而,帶有標準前饋神經網絡(FNN)的深度學習很少有成功的案例。通常表現良好的 FNN 都只是淺層模型,因此不能挖掘多層的抽象表征。所以我們希望引入自歸一化神經網絡(self-normalizing neural networks/SNNs)以幫助挖掘高層次的抽象表征。雖然批歸一化要求較精確的歸一化,但 SNN 的神經元激勵值可以自動地收斂到零均值和單位方差。SNN 的激活函數即稱之為「可縮放指數型線性單元(scaled exponential linear units/SELUs)」,該單元引入了自歸一化的屬性。使用 Banach 的不動點定理(fixed-point theorem),我們證明了激勵值逼近于零均值和單位方差并且通過許多層的前向傳播還是將收斂到零均值和單位方差,即使是存在噪聲和擾動的情況下也是這樣。這種 SNN 收斂屬性就允許 (1) 訓練許多層的深度神經網絡,同時 (2) 采用強正則化、(3) 令學習更具魯棒性。此外,對于不逼近單位方差的激勵值,我們證明了其方差存在上確界和下確界,因此梯度消失和梯度爆炸是不可能出現的。同時我們采取了 (a) 來自 UCI 機器學習庫的 121 個任務,并比較了其在 (b) 新藥發現基準和 (c) 天文學任務上采用標準 FNN 和其他機器學習方法(如隨機森林、支持向量機等)的性能。SNN 在 121 個 UCI 任務上顯著地優于所有競爭的 FNN 方法,并在 Tox21 數據集上超過了所有的競爭方法,同時 SNN 還在天文數據集上達到了新紀錄。該實現的 SNN 架構通常比較深,實現可以在以下鏈接獲得:http://github.com/bioinf-jku/SNNs。
前言
深度學習在許多不同的基準上都達到了新記錄,并促進了各種商業應用的發展 [25, 33]。循環神經網絡(RNN)[18] 令語音和自然語言處理達到了新階段。而與其相對應的卷積神經網絡(CNN)[24] 則變革了計算機視覺和視頻任務。
然而,當我們回顧 Kaggle 競賽時,通常很少有任務是和計算機視覺或序列任務相關的,梯度提升、隨機森林或支持向量機(SVM)通常在絕大多數任務上都能取得十分優秀的表現。相反,深度學習卻表現并不優異。
為了更魯棒地訓練深度卷積神經網絡(CNN),批歸一化發展成了歸一化神經元激勵值為 0 均值和單位方差 [20] 的標準方法。層級歸一化(Layer normalization)[2] 確保了 0 均值和單位方差,因為如果上一層的激勵值有 0 均值和單位方差,那么權值歸一化 [32] 就確保了 0 均值和單位方差。然而,歸一化技術在訓練時通常會受到隨機梯度下降(SGD)、隨機正則化(如 dropout)和估計歸一化參數所擾動。
自歸一化神經網絡(SNN)對于擾動是具有魯棒性的,它在訓練誤差上并沒有高方差(見圖 1)。SNN 令神經元激勵值達到 0 均值和單位方差,從而達到和批歸一化相類似的效果,而這種歸一化效果可以在許多層級的訓練中都保持魯棒性。SNN 基于縮放指數型線性單元(SELU)而引進了自歸一化屬性,因此方差穩定化(variance stabilization)也就避免了梯度爆炸和梯度消失。
自歸一化神經網絡(SNN)
歸一化和 SNN
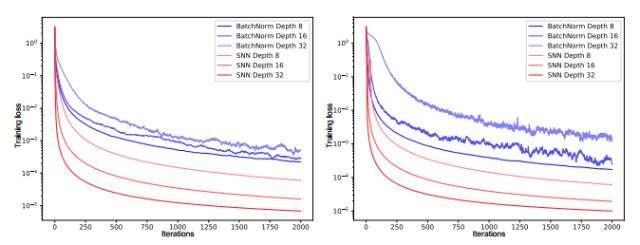
圖 1:左邊圖表和右邊圖表的 y 軸展示了帶有批歸一化(BatchNorm)和自歸一化(SNN)的前饋神經網絡(FNN)的訓練損失,x 軸代表迭代次數,該訓練在 MNIST 數據集和 CIFAR10 數據集上完成。我們測試的神經網絡有 8、16 和 32 層,且學習率為 1e-5。采用批歸一化的 FNN 由于擾動出現了較大的方差,但 SNN 并不會出現較大的方差,因此 SNN 對擾動會更加魯棒,同時學習的速度也會更加迅速。
構建自歸一化神經網絡
我們通過調整函數 g 的屬性以構建自歸一化神經網絡。函數 g 只有兩個可設計的選擇:(1) 激活函數和 (2) 權重的初始化。
通過映射函數 g 派生均值和方差
我們假設 xi 之間相互獨立,并且有相同的均值μ 和方差 ν,當然獨立性假設通常得不到滿足。我們將在后面詳細描述獨立性假設。函數 g 將前一層神經網絡激勵值的均值和方差映射到下一層中激勵值 y 的均值μ? = E(y) 和方差ν? = Var(y) 中:

這些積分的解析解可以通過以下方程求出:
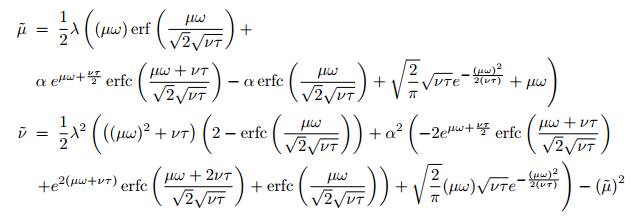
歸一化權值的穩定和誘集不動點(Attracting Fixed Point)(0,1)
非歸一化權值的穩定和誘集不動點(Attracting Fixed Point)
在學習中歸一化的權值向量 w 并得不到保證。

圖 2:對于ω = 0 和 τ = 1,上圖描述了將均值μ(x 軸)和方差 v(y 軸)映射到下一層的均值 μ?和方差ν?。箭頭展示了由 g : (μ, ν) → (?μ, ν?) 映射的 (μ, ν) 的方向。映射 g 的不動點為 (0, 1)。
定理一(穩定和誘集不動點)
該章節給出了定理證明的概要(附錄 Section A3 給出詳細的證明)。根據 Banach 不動點定理(fixed point theorem),我們證明了存在的誘集和穩定不動點。
定理二(降低 v)
該定理的詳細證明可以在附錄 Section A3 中找到。因此,當映射經過許多層級時,在區間 [3, 16] 內的方差被映射到一個小于 3 的值。
定理三(提高 v)
該定理的證明可以在附錄 Section A3 找到。所有映射 g(Eq. (3)) 的不動點 (μ, ν) 確保了 0.8 =< τ時ν ? >0.16,0.9 =< τ時ν ?> 0.24。
初始化
因為 SNN 有歸一化權值的 0 均值和單位方差不動點,所以我們初始化 SNN 來滿足一些期望的約束條件。
新的 Dropout 技術
標準的 Dropout 隨機地設定一個激勵值 x 以 1-q 的概率等于 0,其中 0 < q < 1。為了保持均值,激勵值在訓練中通過 1/q 進行縮放。
中心極限定理和獨立性假設的適用性

實驗(略)
結論
我們提出了自歸一化神經網絡,并且已經證明了當神經元激勵在網絡中傳播時是在朝零均值(zero mean)和單位方差(unit variance)的趨勢發展的。而且,對于沒有接近單位方差的激勵,我們也證明了方差映射的上線和下限。于是 SNN 不會產梯度消失和梯度爆炸的問題。因此,SNN 非常適用于多層的結構,這使我們可以引入一個全新的正則化(regularization)機制,從而更穩健地進行學習。在 121UCI 基準數據集中,SNN 已經超過了其他一些包括或不包括歸一化方法的 FNN,比如批歸一化(batch)、層級歸一化(layer)、權值歸一化(weight normalization)或其它特殊結構(Highway network 或 Residual network)。SNN 也在藥物研發和天文學任務中產生了完美的結果。和其他的 FNN 網絡相比,高性能的 SNN 結構通常深度更深。
附錄(略)
SELU 與 Relu、Leaky Relu 的對比
昨日,Shao-Hua Sun 在 Github 上放出了 SELU 與 Relu、Leaky Relu 的對比,機器之心對比較結果進行了翻譯介紹,具體的實現過程可參看以下項目地址。
項目地址:https://github.com/shaohua0116/Activation-Visualization-Histogram
描述
本實驗包括《自歸一化神經網絡》(Self-Normalizing Neural Networks)這篇論文提出的 SELUs(縮放指數型線性單元)的 Tensorflow 實現。也旨在對 SELUs,ReLU 和 Leaky-ReLU 等進行對比。本實驗的重點是在 Tensorboard 上對激勵進行可視化。
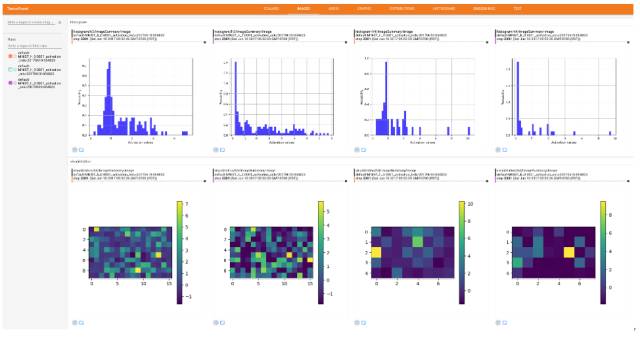
SELUs(縮放指數型線性單元),ReLU 和 Leaky-ReLU 的可視化和直方圖對比
理論上,我們希望每一層的激勵的均值為 0(zero mean),方差為 1(unit variance),來使在各層之間傳播的張量收斂(均值為 0,方差為 1)。這樣一來就避免了梯度突然消失或爆炸性增長的問題,從而使學習過程更加穩定。在本實驗中,作者提出 SELUs(縮放指數型線性單元),旨在對神經元激勵進行自動地轉移(shift)和重縮放 (rescale),在沒有明確的歸一化的情況下去實現零均值和單位方差。
為了用實驗證明所提出的激勵的有效性,一個包含三個卷積層的卷積神經網絡(也包括三個完全連接層——fully connected layers)在 MNIST, SVHN 和 CIFAR10 數據集上進行訓練,來進行圖像分類。為了克服 Tensorboard 顯示內容的一些限制,我們引入了繪圖庫 Tensorflow Plot 來彌補 Python 繪圖庫和 Tensorboard 間的差距。以下是一些例子。
在 Tensorboard 上的激勵值直方圖

在 Tensorboard 上的激勵值可視化
實現模型在三個公開的數據集上進行的訓練與測試:MNIST、SVHN 和 CIFAR-10。
結果
下面我們只選擇性展示了最后一個卷積層(第三層)和較早的全連接層(第四層)的直方圖和可視化激勵值圖。
SELU
卷積層
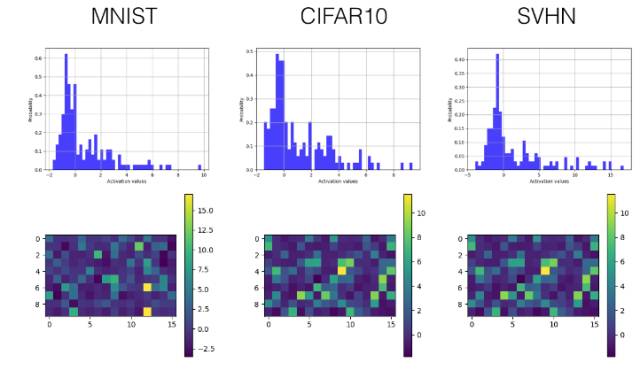
全連接層
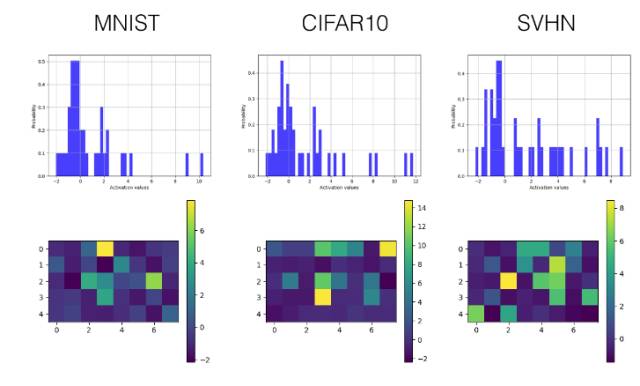
ReLU
卷積層
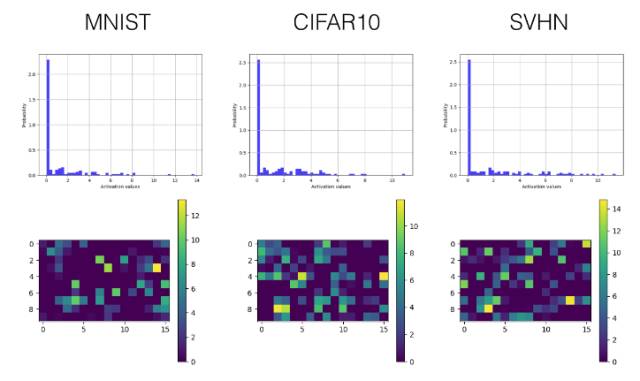
全連接層
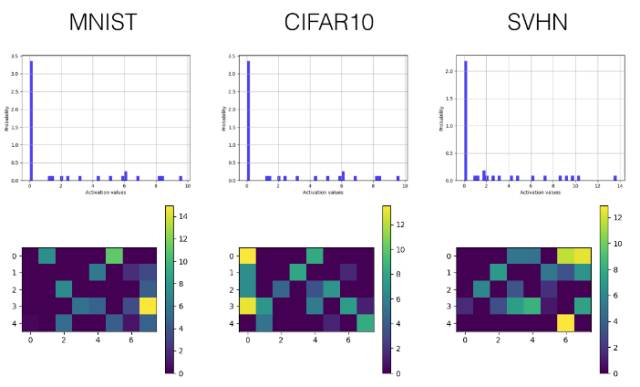
Leaky ReLU
卷積層
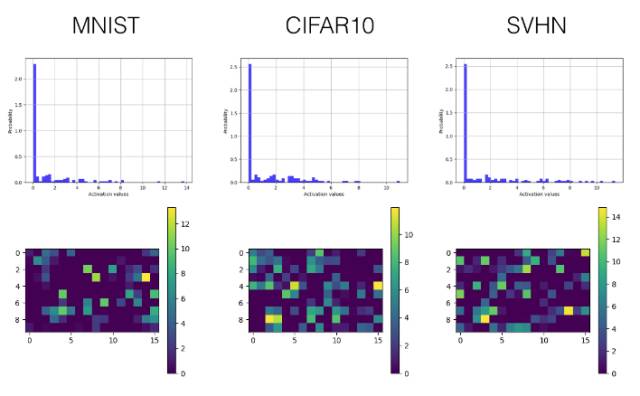
全連接層
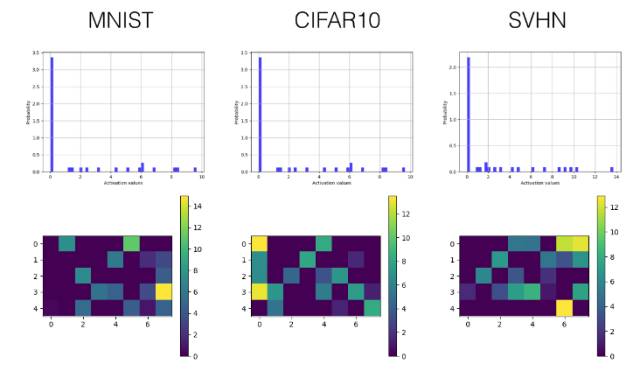
相關工作
Self-Normalizing Neural Networks by Klambauer et. al
Rectified Linear Units Improve Restricted Boltzmann Machines by Nair et. al.
Empirical Evaluation of Rectified Activations in Convolutional Network by Xu et. al.
作者
Shao-Hua Sun / @shaohua0116 (https://shaohua0116.github.io/)。
歡迎加入本站公開興趣群商業智能與數據分析群
興趣范圍包括各種讓數據產生價值的辦法,實際應用案例分享與討論,分析工具,ETL工具,數據倉庫,數據挖掘工具,報表系統等全方位知識
QQ群:81035754
文章版權歸作者所有,未經允許請勿轉載,若此文章存在違規行為,您可以聯系管理員刪除。
轉載請注明本文地址:http://m.specialneedsforspecialkids.com/yun/4572.html
摘要:修正線性單元,是神經網絡中最常用的激活函數。顧名思義,值激活函數返回輸入的值。如同余弦函數,或簡單正弦函數激活函數為神經網絡引入了周期性。此外,激活函數為零點對稱的奇函數。 在神經網絡中,激活函數決定來自給定輸入集的節點的輸出,其中非線性激活函數允許網絡復制復雜的非線性行為。正如絕大多數神經網絡借助某種形式的梯度下降進行優化,激活函數需要是可微分(或者至少是幾乎完全可微分的)。此外,復雜的激...
摘要:為了解決這個問題出現了批量歸一化的算法,他對每一層的輸入進行歸一化,保證每層的輸入數據分布是穩定的,從而加速訓練批量歸一化歸一化批,一批樣本輸入,,個樣本與激活函數層卷積層全連接層池化層一樣,批量歸一化也屬于網絡的一層,簡稱。 【DL-CV】數據預處理&權重初始化【DL-CV】正則化,Dropout 先來交代一下背景:在網絡訓練的過程中,參數的更新會導致網絡的各層輸入數據的分布不斷變化...
摘要:為了解決這個問題出現了批量歸一化的算法,他對每一層的輸入進行歸一化,保證每層的輸入數據分布是穩定的,從而加速訓練批量歸一化歸一化批,一批樣本輸入,,個樣本與激活函數層卷積層全連接層池化層一樣,批量歸一化也屬于網絡的一層,簡稱。 【DL-CV】數據預處理&權重初始化【DL-CV】正則化,Dropout 先來交代一下背景:在網絡訓練的過程中,參數的更新會導致網絡的各層輸入數據的分布不斷變化...
閱讀 2753·2021-11-19 09:40
閱讀 5321·2021-09-27 14:10
閱讀 2107·2021-09-04 16:45
閱讀 1479·2021-07-25 21:37
閱讀 3003·2019-08-30 10:57
閱讀 2987·2019-08-28 17:59
閱讀 1062·2019-08-26 13:46
閱讀 1414·2019-08-26 13:27