摘要：在實踐中，幾乎總是通過向梯度增加來實現算法，而不是真正改變損失函數。顯然這是兩種不同的方法。那么，權重衰減是不是總比的正則化更好呢我們還沒發現明顯更糟的情況，但無論是遷移學習問題例如斯坦福汽車數據集上的的微調還是

跌宕起伏的 Adam

縱觀 Adam 優化器的發展歷程，就像過山車一樣。它于 2014 年在論文 Adam: A Method for Stochastic Optimization（https://arxiv.org/abs/1412.6980 ）中首次提出，其核心是一個簡單而直觀的想法：既然我們明確地知道某些參數需要移動得更快、更遠，那為什么每個參數還要遵循相同的學習率呢？因為最近梯度的平方告訴我們每增加一個權重可以得到多少個信號，所以我們可以除以它來確保即使是最緩慢的權重也能獲得“發光”的機會。Adam 接受了這個想法，在過程中增加了標準方法，Adam 優化器就這樣誕生了。它需要稍微調整來避免早期批出現偏差。

當論文首次發布時，原論文中的一些圖表（如下圖所示）讓深度學習社區感到興奮不已：

Adam 和其他優化器的對比

訓練速度加快了 200%！

“總體來看，我們發現 Adam 非常強大，非常適用于時下機器學習領域中的各種非凸優化問題。”論文如此總結道。那是三年前深度學習最輝煌的時候。但事情后來并沒有像我們所期望的那樣發展，很少見到有研究文章使用 Adam 來訓練模型，新的研究也開始明顯地不鼓勵使用 Adam（如論文 The Marginal Value of Adaptive Gradient Methods in Machine Learning，https://arxiv.org/abs/1705.08292 ），并通過幾個實驗結果表明，普通的 SGD+Momentum 可能比復雜的 Adam 表現更好。在 2018 年 fast.ai 的課程中，可憐的 Adam 就被從早期課程中剔除了。

但在 2017 年底，Adam 似乎獲得了重生。Ilya Loshchilov 和 Frank Hutter 在他們的論文 Fixing Weight Decay Regularization in Adam（https://arxiv.org/abs/1711.05101 ）中指出，在每個庫中在 Adam 上實施的權重衰減似乎都是錯誤的，并提出了一種簡單的方法（他們稱之為 AdamW）來修復這個問題。雖然他們的結果略有不同，但是他們確實給出了一些令人鼓舞的圖表，如下圖所示：

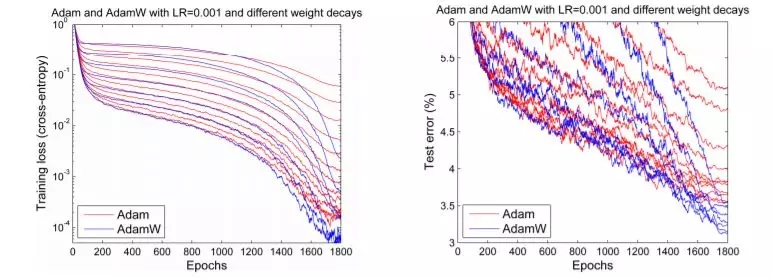
Adam 和 AdamW 對比

我們期待人們能夠對 Adam 重燃熱情，因為它的一些早期結果似乎已經可以重現。但事實并非如此。應用它的一個深度學習框架是 fastai，使用的是 Sylvain 編寫的代碼。但因為缺乏可用的通用框架，日常實踐者就被又舊又難用的 Adam 所困。

但這并不是問題，前方還有更多的障礙。有兩篇論文分別指出了 Adam 在收斂性證明方面存在明顯的問題。盡管其中一篇論文提出了解決方案（并在久負盛名的 ICLR 大會上獲得了“較佳論文”獎），他們稱之為_AMSGrad_。但是，如果要說我們從這段充滿戲劇化的生活（至少按照優化器的標準而言是戲劇化的）中學到了什么，那就是，沒有什么是表面看到的那樣。事實上，博士生 Jeremy Bernstein 在博文 On the Convergence of Adam and Beyond（https://openreview.net/forum?id=ryQu7f-RZ?eId=B1PDZUChG ）中指出，所謂的收斂問題實際上只是超參數選擇不當，也許 AMSGrad 并不能解決問題。另一名博士生 Filip Korzeniowski 在論文 Experiments with AMSGrad（https://fdlm.github.io/post/amsgrad/ ） 中展示了一些早期研究成果，似乎也證明了這個令人沮喪的觀點。

Adam 到底怎么樣？

對于那些只想快速訓練較精確模型的人，我們該做些什么呢？讓我們用數百年來解決科學辯論的方式來解決這一爭議：做實驗！

我們將在本文稍后闡述所有的細節，但先讓我們看一下大致結果：

適當調參之后，Adam 真的是能用的！我們在各種任務上獲得了訓練時間方面的結果如下：

在含有測試時間增加的 18 個 epoch 或 30 個 epoch 訓練 CIFAR10，使其準確率超過 94%，如 DAWNBech 競賽；

只需 60 個 epoch 即可對 Resnet50 進行調參，使其在斯坦福汽車數據集的準確率達到 90%，據報告稱，之前要達到相同的準確率需 600 個 epoch；

從零開始訓練 AWD LSTM 或 QRNN（見論文 Regularizing and Optimizing LSTM Language Models，https://arxiv.org/abs/1708.02182 ），需 90 個 epoch（或在單個 GPU 上訓練一個半小時），其困惑度在 Wikitext-2 達到當前最優水平，據之前報告稱，LSTM 需要 750 個 epoch，QRNN 需要 500 個 epoch。

這意味著我們已經看到了使用 Adam 的超收斂！（參見論文 Super-Convergence: Very Fast Training of Neural Networks Using Large Learning Rates，https://arxiv.org/abs/1708.07120 ）超收斂是訓練學習率高的神經網絡時出現的一種現象，表示節約了一半的訓練時間。在人們了解 AdamW 之前，人們訓練 CIFAR10 使其準確率達到 94% 需要大約 100 個 epoch。

與之前的工作相比，我們發現只要調整得當，Adam 在嘗試過的每一個 CNN 圖像問題上都能獲得與 SGD+Momentum 一樣的準確率，而且，幾乎總是快一點。

至于有人認為 AMSGrad 是一個槽糕的“解決方案”，這種看法是正確的。我們一直發現，AMSGrad 的準確率（或其他相關指標）并沒有獲得比普通的 Adam/AdamW 更高的增益。

如果你聽到人們說 Adam 的泛化性能不如 SGD+Momentum 時，你基本就會發現他們為自己的模型選擇的超參數其實蠻糟糕的。通常情況下，Adam 需要比 SGD 更多的正則化，因此，當從 SGD 轉向到 Adam 時，一定要確保調整正則化超參數。

AdamW

理解 AdamW：權重衰減與 L2 正則化

L2 正則化是減少過擬合的經典方法，它向損失函數添加模型的所有權重的平方和組成的懲罰項，乘以特定的超參數來控制懲罰力度（在本文中，所有的方程式均使用 Python、NumPy 和 PyTorch 表示法）：

final_loss = loss + wd * all_weights.pow(2).sum() / 2

其中，wd是我們設置的超參數，也可稱為權重衰減，因為運用 vanilla SGD 時，它相當于使用如下方程式更新權重：

w = w - lr * w.grad - lr * wd * w

其中，lr表示學習率，w2表示損失函數對w的導數，wd*w表示懲罰項對w的求導結果。在這個方程式中，我們可以看到每一次更新都會減去一小部分權重，因此這就是命名為“衰減”的原因。

我們注意到所有的庫都使用了第一種形式。在實踐中，幾乎總是通過向梯度增加wd*d來實現算法，而不是真正改變損失函數。因為我們不希望還有其他更簡單的方法的情況下，增加額外的計算量來修正損失。

如果這兩個概念是一樣的話，那為什么還要區分這兩種概念呢？答案就是，它們對于 vanilla SGD 來說是等價的，一旦我們添加動量，或者使用像 Adam 那樣復雜的最優化器，那么 L2 正則化（第一個方程式）和權重衰減（第二個方程式）就會變得不同。在本文其余部分中，我們討論的權重衰減都是指第二個方程式（權重將會衰減一點），而我們討論經典方法時就會討論 L2 正則化。

讓我們來看看帶動量的 SGD。使用 L2 正則化會在梯度上添加wd*d（正如我們前面所述），但梯度并不是直接從權重中減去。首先我們要計算一個移動均值：

moving_avg = alpha * moving_avg + (1-alpha) * (w.grad + wd*w)

這個移動均值乘以學習率，再減去w得到權重的更新，因此w與正則化相關的部分是lr*(1-alpha)*wd*d加上已經在moving_avg中前面權重的結合。

因此，權重衰減的更新方式可以如下表示：

moving_avg = alpha * moving_avg + (1-alpha) * w.grad?

w = w - lr * moving_avg - lr * wd * w

我們可以看到，從w連接到正則化的部分在兩種方法是不一樣的。在使用 Adam 優化器時，權重衰減的部分可能相差很大：在 L2 正則化的情況下，我們將這個wd*d添加到梯度中，然后分別計算梯度機器平方的移動均值，然后再更新權重。然而權重衰減方法只是簡單地更新權重，然后每次從權重中減去一點。

顯然這是兩種不同的方法。在進行實驗之后，Ilya Loshchilov 和 Frank Hutter 在論文中建議我們應該使用 Adam 的權重衰減方法，而不是像經典深度學習庫中實現的 L2 正則化方法。

實現 AdamW

那我們要怎么做才能實現 AdamW 呢？如果你在使用 fastai 庫，那么在使用 fit 函數時只需添加參數use_wd_sched=True就能簡單地實現了：

learn.fit(lr, 1, wds=1e-4, use_wd_sched=True)

如果你更青睞新的訓練 API，那你可以在每個訓練階段中使用參數wd_loss=False（用于在衰減過程中沒有計算的權重衰減）：

phases = [TrainingPhase(1, optim.Adam, lr, wds=1-e4, wd_loss=False)]

learn.fit_opt_sched(phases)

以下是我們在 fastai 中如何實現 AdamW 的簡要總結。在優化器中的階躍函數（step function）中，只需使用梯度修正參數，根本不使用參數本身的值（除了權重衰減，我們將在外部處理）。我們可以在最優化器步驟之前通過簡單的實現權重衰減，但這仍然需要在計算梯度之后才能完成，否則會影響梯度值。因此在訓練循環中，我們必須確定計算權重衰減的位置。

loss.backward()

#Do the weight decay here!

optimizer.step()

當然，最優化器應該設定為 wd=0，否則它還會做一些 L2 正則化，這也是我們不希望看到的。現在在權重衰減的位置中，我們可以在所有參數上進行循環，并依次采用權重衰減的更新。我們的參數應該存儲在優化器的字典param_groups中，因此這個循環應該如下段代碼所示那樣的：

loss.backward()

for group in optimizer.param_groups():

? ?for param in group["params"]:

? ? ? ?param.data = param.data.add(-wd * group["lr"], param.data)

optimizer.step()

AdamW 實驗結果：是否有效？

我們先在計算機視覺問題上進行了測試，結果令人鼓舞。具體來說，我們使用 Adam 和 L2 正則化在 30 個 epoch（這是 SGD 在 1cycle 策略（詳見 https://sgugger.github.io/the-1cycle-policy.html）中達到 94% 準確率的必要時間）獲得的準確率平均為 93.36%，在兩次中有一次超過了 94%。當使用 Adam 和權重衰減方法時，我們始終得到的是 94%~94.25% 的準確率。為此，我們發現使用 1cycle 策略時，beta2 的最優值為 0.99。我們將 beta1 參數作為 SGD 的動量，也就是說，隨著學習率的增長，它從 0.95 降到 0.85，然后隨著學習率的降低又升到 0.95。

L2 正則化或權重衰減準確率

更令人印象深刻的是，使用測試時間增加（即對測試集的一個圖像和它的四個數據增強版本進行預測的平均值），我們可以在僅僅 18 個 epoch 內達到 94% 的準確率（平均 93.98%）！使用簡單的 Adam 和 L2 正則化的話，每嘗試 20 個 epoch 就會出現一次超過 94% 的情況。

在這些比較中需要考慮的一件事是，改變正則化的方式會改變權重衰減或學習率的較佳值。在我們進行的測試中，L2 正則化的較佳學習率為 1e-6（較大學習率為 1e-3），而 0.3 是權重衰減的較佳值（學習率為 3e-3）。在我們的測試中，數量級的差異都是非常一致的，主要是因為 L2 正則化被梯度的平均范數（相當低）有效地劃分，并且 Adam 的學習率相當小（所以權重衰減的更新需要更強的系數）。

那么，權重衰減是不是總比 Adam 的 L2 正則化更好呢？我們還沒發現明顯更糟的情況，但無論是遷移學習問題（例如斯坦福汽車數據集上的 Resnet50 的微調）還是 RNN，它都沒有給出更好的結果。

AMSGrad

理解 AMSGrad

AMSGrad 是由 Sashank J. Reddi、Satyen Kale 和 Sanjiv Kumar 在最近的一篇文章 On the Convergence of Adam and Beyond（https://openreview.net/forum?id=ryQu7f-RZ ）中介紹的。通過分析 Adam 優化器的收斂性證明，他們發現了更新規則中的一個錯誤，該錯誤可能導致算法收斂到次優點。他們設計了理論實驗，展示了 Adam 失敗的情形，并提出了一個簡單的解決方案。

為了更好地理解錯誤和解決方案，讓我們看一下 Adam 的更新規則：

avg_grads = beta1 * avg_grads + (1-beta1) * w.grad

avg_squared = beta2 * (avg_squared) + (1-beta2) * (w.grad ** 2)

w = w - lr * avg_grads / sqrt(avg_squared)

我們剛剛跳過了偏差修正（這對訓練的開始很有用) 來關注重點。作者發現的 Adam 收斂性證明中的錯誤之處在于它需要數量。

lr / sqrt(avg_squared）

這是我們朝著平均梯度方向邁出的一步，在訓練中逐漸減少。由于學習率通常是常量或遞減的（除了像我們這樣瘋狂的人試圖獲得超收斂之外），作者提出的解決方案是通過添加另一個變量來跟蹤它們的較大值來迫使avg_square量增加。

實現 AMSGrad

相關文章在 ICLR 2018 中獲得了一項大獎，并已經在兩個主要的深度學習庫——PyTorch 和 Keras 中實現了。所以我們只要傳入參數amsgrad=True就萬事大吉了。

前一節中的權重更新代碼更改為如下內容:

avg_grads = beta1 * avg_grads + (1-beta1) * w.grad

avg_squared = beta2 * (avg_squared) + (1-beta2) * (w.grad ** 2)

max_squared = max(avg_squared, max_squared)

w = w - lr * avg_grads / sqrt(max_squared)

AMSGrad 實驗結果：大量毫無意義的噪音

AMSGrad 的表現令人失望。我們發現，在所有的實驗中，它一點用都沒有。即使 AMSGrad 發現的最小值確實有時比 Adam 達到的最小值略低（在損失方面），其度量（準確率、f1 分數等）最終總是更槽糕（請訪問此網址參閱更多表格和示例：https://fdlm.github.io/post/amsgrad/ ）

Adam 優化器在深度學習中收斂的證明（因為它是針對凸問題的）和他們在其中發現的錯誤對于與現實問題無關的合成實驗很重要。實際的測試表明，當那些avg_squared梯度想要減少時，這樣做能得到較好的結果。

這表明，即使對理論的關注對獲得一些新想法很有用，也沒有什么能代替實驗（以及大量的實驗），以確保這些想法能夠幫助實踐者訓練更好的模型。

附錄: 全部結果

從零開始訓練 CIFAR10（模型是一個 WideResnet 22，如下表所示為五個模型的測試集中平均誤差結果）：

使用 fastai 庫引入的標準頭對斯坦福汽車數據集上的 Resnet50 進行微調（在解凍前對頭進行 20 個 epoch 的訓練，并用不同的學習率訓練 40 個 epoch）：

使用 github repo 中的超參數（https://github.com/salesforce/awd-lstm-lm ）對 AWD LSTM 進行訓練（結果顯示在有無緩存指針的情況下驗證 / 測試集的困惑度）：

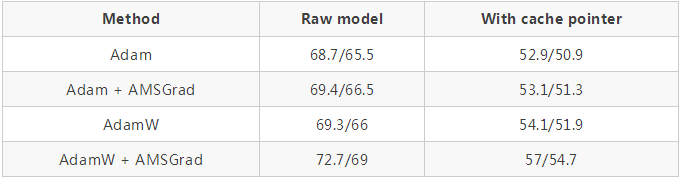
QRNNs 代替 LSTMs 也一樣：

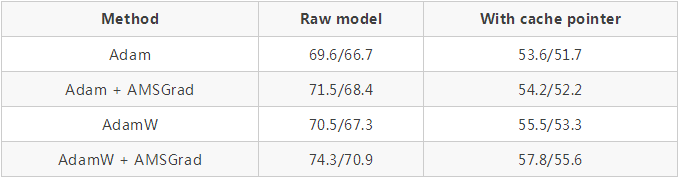
對于這個特定的任務，我們使用了一個改進版本的 1cycle 策略，加快了學習速度，之后長時間保持較高的恒定學習速度，然后再次下降。

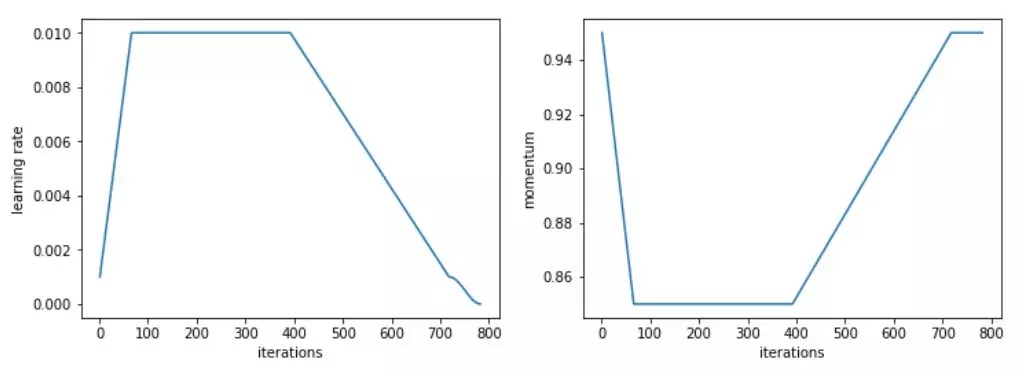
Adam 和其他優化器之間的對比

所有相關超參數的值以及用于生成這些結果的代碼可訪問此網址來獲得：

https://github.com/sgugger/Adam-experiments

原文鏈接：

AdamW and Super-convergence is now the fastest way to train neural nets

http://www.fast.ai/2018/07/02/adam-weight-decay/

聲明：文章收集于網絡，如有侵權，請聯系小編及時處理，謝謝！

商業智能與數據分析群

興趣范圍包括各種讓數據產生價值的辦法，實際應用案例分享與討論，分析工具，ETL工具，數據倉庫，數據挖掘工具，報表系統等全方位知識

QQ群：81035754